
| Introduction du cosinus |
| Clg Ausone, Bazas Groupe Math&Info, Bordeaux, juin 2001 |
Niveau
Classe de quatrième.
Objectifs
Introduction du cosinus.
Prérequis
Aucun.
Organisation pratique
Une salle équipée d'un ordinateur muni d'un écran rétro-projetable. Le logiciel
Géoplan pour Windows.
Une fiche d’activité préparatoire.
Le professeur réalise au préalable l’imagiciel décrit en annexe. Celui-ci montre
un triangle variable, permet d’afficher la valeur d’un angle et le cosinus correspondant.
Il permet également de tracer la courbe représentant la fonction cosinus sur
l’intervalle [0 ; 90].
Description
La séance est une heure de cours classique, mais avec utilisation
d’une tablette à rétroprojeter.
Les élèves arrivent en classe après avoir réalisé une activité préparatoire.
Le travail sur ordinateur permet de vérifier les hypothèses que l'on peut faire
à partir du travail des élèves et de tracer la courbe du cosinus.
Le logiciel Géoplan permet de montrer l'influence de l'angle sur la valeur du
quotient AB/AC, et de vérifier que seul cet angle influe sur ce rapport.
Bilan
L'informatique apporte une plus grande variété de situation, un gain de temps par rapport à des figures faites de façon classique au tableau et une plus grande précision dans le tracé et les mesures (tout au moins en apparence).
Les élèves constatent que, dans un triangle rectangle, le rapport du côté adjacent sur l'hypoténuse ne dépend pas de la taille du triangle mais seulement de l'angle. Le même travail, réalisé jusqu'alors à partir de leurs calculs était moins convaincant car, en raison de l'imprécision des dessins et des mesures, l'égalité des différents rapports, pour un angle donné, n'était qu'approximative.
Fiche élève
Activité préparatoires
1. Tracer 8 triangles ABC rectangles en B et tels que l'angle en A
mesure successivement 10°, 20°, ...., 80°.
Mesurer les longueurs AB et AC et compléter le tableau ci-dessous.
| 10° |
20° |
30° |
40° |
50° |
60° |
70° |
80° |
|
| AB |
||||||||
| AC |
||||||||
| AB/AC |
Quelles remarques peut-on faire ?
2. Sur un graphique (unité 2 cm pour 10° sur l'axe des abscisses, et 10 cm pour une unité sur l'axe des ordonnées) placer les points ayant pour abscisse la mesure de l'angle en A, et pour ordonnée la valeur du rapport AB/AC.
Définition du cosinus

Annexe : La figure (cosinus.g2w) et son utilisation
Conception de la figure.
On réalise un imagiciel qui, dans un premier cadre, montre un triangle ABC rectangle en B dans lequel on peut modifier le point B et l’angle A et, dans un deuxième cadre, trace la courbe de la fonction cosinus sur l’intervalle [ 0 ; 90 ].
Pour cela, on définit d’abord deux cadres c1 et c2 de diagonales respectives M1M2 et M3M2 (coordonnées par rapport au repère de base : M1(-10 ; 6), M2(-0.5 ; -5), M3(0.5 ; 6), M4(10 ; -5) ).
On définit ensuite les points A(-9 ; -4) et B1 (-1 ; -4) (qui se trouvent dans le premier cadre), la demi-droite [AB1) et un point B mobile sur la demi-droite [AB1).
Pour l’angle, on définit une variable entière libre, ang, entre 0 et 90, puis le point C1 image de B1 par rotation de centre A et d’angle ang (en degré).
On définit C comme intersection de la perpendiculaire d1 à (AB) passant par B et de la droite (AC1)
On masque ensuite les éléments inutiles : M1, M2, M3, M4, B1, C1, d1.
Les seuls éléments visibles sont alors les 2 cadres et les points ABC
On trace les segments AB, BC, AC et on limite ces tracés au cadre c1.
On prévoit l’affichage de ang, des longueurs de AB, de AC, ainsi que leur rapport, rap
On définit un repère dans le cadre c2 : origine O(1 ; -4), premier vecteur : 0.1* vec(i), deuxième vecteur : 8*vec(j), une graduation toutes les 10 unités en abscisse et toutes les 0,1 unité en ordonnée. On peut quadriller ce repère. On le limite au cadre c2.
On définit alors le point K (ang ; rap) dans le nouveau repère.
En mode trace, le point K décrit la courbe de la fonction cosinus lorsque l’on pilote ang au clavier.
Il est possible de créer des commandes qui permettront de faire apparaître successivement le cadre c1 et son contenu, le cadre c2 vide, puis le repère, puis le point K.
Dans le fichier Géoplan joint, plusieurs commandes sont disponibles :
A permet de piloter l'angle
B permet de piloter B
Ctrl-D permet de montrer ou de cacher le graphique.
Ctrl-L trace le lieu du point K
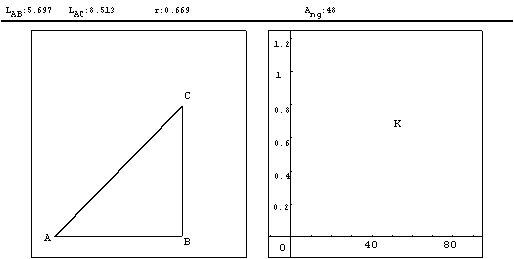
Dans un premier temps on n’affiche par le graphique.
Pour montrer que le rapport ne dépend pas de la « taille » du triangle mais uniquement de la mesure de l’angle, il suffit de piloter le point B (appuyer sur la touche B, puis piloter avec les flèches du clavier)…
Le rapport est une fonction décroissante de l’angle. En modifiant la valeur de l’angle (appuyer sur la touche A, puis piloter avec les flèches du clavier), on peut faire constater que la valeur du rapport diminue lorsque l’angle augmente. On peut alors faire afficher le graphique (Ctrl-D) puis faire tracer le lieu du point K. Sur ce graphique, on a en abscisse la valeur de l’angle en degrés, et en ordonnée la valeur du rapport. Le point K laisse une trace, on peut donc constater que la fonction est décroissante et non linéaire, que le rapport est compris entre 0 et 1.