Applications affines et géométrie |
Collège Max Linder, St Loubes (33) |
Niveau
Troisième.
Objectifs
Dans chacun des cas, le principe est de montrer aux élèves la relation entre un phénomène concret et une représentation graphique.
Prérequis
Applications affines.
Organisation pratique
Ordinateur « tableau noir ».
Les exercices ont été préparés à la maison. Il s’agit ici d’une séquence de
correction.
Description
C’est une séquence de correction d’exercices préparés à la
maison. Le logiciel géoplan permet de visualiser les variations de grandeurs
géométriques.
Le professeur a créé l’imagiciel avant le cours et a défini des commandes. Ainsi,
on peut faire apparaître le tracé de la courbe en appuyant sur CTRL L et un
rappel des coordonnées des points de la courbe grâce à la commande CTRL A.
On pourrait très bien concevoir cette activité sous forme de travaux pratiques,
sous réserve de pouvoir dédoubler la classe et de disposer de suffisamment de
matériel.
Bilan
Les élèves se sont montrés vivement intéressés.
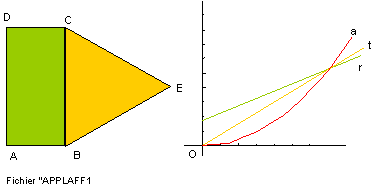
Soit ABCD un rectangle qui a pour dimension AB =3,5 cm et BC = x (en centimètre). Soit BCE un triangle équilatéral.
1) Expliquer pourquoi le périmètre r du rectangle est une application affine de x.
2) Expliquer pourquoi le périmètre t du triangle est une application linéaire de x.
3) L'aire a du triangle est elle une application affine de x ? Pourquoi ?
4) Pour quelle valeur de x le périmètre du rectangle est-il égal au périmètre du triangle.
5) Pour quelles valeur de x le périmètre du triangle est-il plus petit que le périmètre du rectangle ?

Correction et remarques sur cet exercice
Le périmètre du rectangle est : r = 2x + 7. C'est une application affine
Le périmètre du triangle est t = 3x. C'est une application linéaire.
L'aire du triangle est
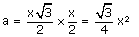 .
.
Ce n'est ni l'un ni l'autre.
En regardant la figure on pourrait croire que les trois tracés se croisent en un seul point. Il n'en est rien.
Le périmètre du rectangle et le périmètre du triangle sont égaux si x = 7 cm.
L'aire et le périmètre du triangle on la même valeur si 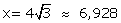 .
.
Une nouvelle occasion de montrer les limites de la lecture graphique.
Fichier APPLAFF2
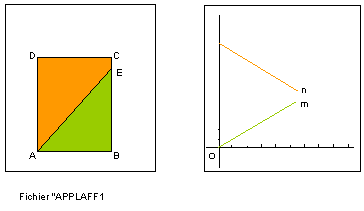
Soit ABCD un rectangle dont la longueur est AD = 6 cm et la largeur AB = 4 cm. Soit E un point du segment CD. On note en centimètre BE = x.
1) Expliquer pourquoi l'aire du triangle ABE est une application affine de x.
2) Expliquer pourquoi l'aire de ADCE est une application affine de x.
3) Représenter graphiquement ces deux applications affines.
4) Déterminer la valeur de x pour laquelle les deux aires sont égales.
Fichier APPLAFF3
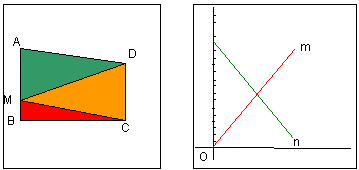
ABCD un trapèze rectangle (B = 90° et C = 90°)
On sait en centimètre : AB = 5, CD = 6 et AD = 4
M est un point du segment [AD] ; on note en centimètres AM = x.
1) Quelles sont les valeurs possibles de x ?
2) Expliquer pourquoi l'aire du triangle ADM est une fonction affine
de x
Expliquer pourquoi l'aire du triangle MCD est une fonction affine de x.
Expliquer pourquoi l'aire du triangle BMC est une fonction affine de x.
3) Dans un même repère représenter graphiquement les trois fonctions affines précédentes.
4) Lire graphiquement dans chacun des cas la valeur de x pour laquelle
:
- Le triangle ADM et MCD ont la même aire ;
- Le triangle BMC et MCD ont la même aire.
Est-il possible que les triangles ADM et BMC aient la même aire ?
5) Retrouver les résultats de la question 4 par le calcul.