| Un problème d’optimisation |
|
Équipe académique mathématiques
Bordeaux, juin 2002 |
| |
Niveau
Classe de Troisième.
Objectifs
Traiter un type de problème peu fréquenté en collège.
Prérequis
Cette activité mobilisant plusieurs champs de compétences est
envisageable en fin d’année de Troisième.
Organisation pratique
Une salle équipée d'un ordinateur muni d'un écran rétroprojetable.
Le logiciel Géoplan pour Windows.
Le professeur réalise au préalable l’imagiciel. Celui-ci permet
l’illustration dynamique de la situation envisagée et facilite la démarche de
conjecture.
Une “ fiche élève ” propose ensuite de démontrer le
résultat pressenti.
Description
La séance se déroule au cours d’une heure de cours traditionnelle.
La partie I (énoncé du problème) de la “ fiche élève ”
est distribuée.
L’imagiciel est ensuite utilisé comme outil au cours d’une séquence
de travail à l’oral. Il permet de poser le problème et favorise la démarche
de conjecture.
La partie II de la “ fiche élève ” est alors distribuée :
Il s’agit d’émettre par écrit la conjecture suggérée par l’activité précédente,
puis de démontrer l’assertion et de terminer le problème. Ce travail, commencé
en classe, est proposé en devoir à la maison.
Fiche élève partie I
(distribuée en début de séance)
| Énoncé
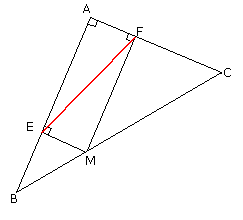
Le triangle ABC est rectangle en A.
On donne : AB = 8 et AC = 6 (les mesures des longueurs étant exprimées
en centimètres)
M est un point de l’hypoténuse [BC].
La perpendiculaire à (AB) passant par M coupe [AB] en E.
La perpendiculaire à (AC) passant par M coupe [AC] en F.
Où doit-on placer le point M pour que la distance EF soit la plus petite
possible ? |
|
Fiche élève partie II
(distribuée après la séquence orale utilisant l’imagiciel)
1. Rappeler la conjecture émise lors de l’activité orale.
2. Démontrer que le quadrilatère AEMF est un rectangle.
En déduire AM = EF.
3. Construire le point H du segment [BC] tel que la longueur AH soit
la plus petite possible.
En déduire la position du point M pour que la distance EF soit la
plus petite possible.
4. Calculer l’aire du triangle ABC.
Calculer BC.
En déduire AH.
5. Quelle est la plus petite valeur prise par la longueur EF lorsque
M se déplace sur le segment [BC] ?
Séquence de travail à l’oral utilisant l’imagiciel
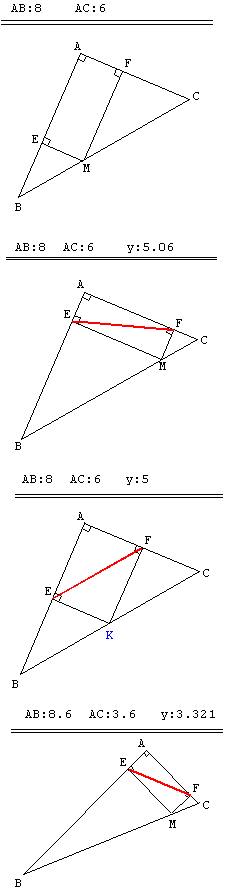
| 1. Écran initial
Triangle ABC rectangle en A.
Affichage des longueurs AB et AC.
2. Commande M :
Point M mobile sur [BC] pilotable au clavier.
Point E pied de la perpendiculaire à (AB) passant par M.
Point F pied de la perpendiculaire à (AC) passant par M.
L’expérience graphique que font les élèves en observant
une figure dont on déplace un élément variable (le point M) les éclaire
sur la nature du problème posé. La permanence d’un rectangle apparaît
… (cf. Documents d’accompagnement des Programmes de Troisième page 12).
3. Commande D :
Diagonale [EF].
Commande y :
Affichage d’une valeur arrondie à 0,001 près de la longueur EF notée
y.
Le logiciel permet alors de faire constater que la distance
EF varie effectivement lorsque M se déplace sur [BC]. Il permet aussi
d’invalider la conjecture fréquemment émise du milieu K de [BC] …
4. Commande K :
Création du point K milieu de [BC].
Commande CTRL K :
Affectation du point M en K.
… cette suggestion d’élève peut permettre de revisiter
la “ droite des milieux dans un triangle ”.
On peut ensuite, par essais successifs, en observant les
valeurs prises par y, “localiser” la position de M répondant à la question.
Pour envisager le cas d’autres triangles rectangles …
5. Commande C :
Sélection pour pilotage au clavier, permet de faire varier AB.
Commande B :
Sélection pour pilotage au clavier, permet de faire varier AC.
Commande CTRL X :
Permet de nouveau de piloter M.
Commande 0 :
Permet de retrouver le triangle rectangle initial.
L’activité de conjecture peut suggérer une exploitation
graphique :
En notant x la longueur BM, le logiciel permet d’obtenir
dans un repère (O, I, J) quelques points de la représentation graphique
de la fonction qui à x associe y. |
|
6. Commande X :
Affichage de la longueur x du segment [BM].
(Si l’on a préalablement modifié les valeurs de b ou de c par pilotage au
clavier, veiller à “reprendre la main” par Commande CTRL X pour
piloter de nouveau M).
Commande G :
Création d’un repère (O, I, J) orthogonal.(Les points I et J sont pilotables
à la souris si l’on veut changer d’unité).
Point N(x,y) dans le repère (O, I, J).
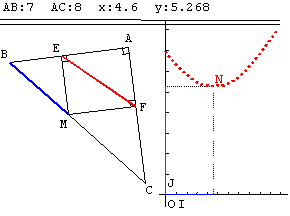
| Le pilotage de
M (donc de x) active la figure et la représentation graphique.
Le pas de variation de x (0 £
x £ 10) fixé ici à 0,2, permet la visualisation
de 51 positions de M (donc de N).
Le rôle des coordonnées d’un point appartenant à la représentation
graphique d’une fonction se trouve clarifié par ce type d’activité offrant
en parallèle une situation géométrique et son exploitation fonctionnelle
induite.
Commande Trace :
Permet d’obtenir la trace de N.
On “affine” ainsi la localisation de la position du point
M qui minimise la longueur y = EF.
Commande N :
Permet , le mode trace étant désactivé, de retrouver les points de la
représentation graphique.
L’examen de plusieurs cas de figure (en modifiant les
longueurs AB et AC comme indiqué § 5), permet de préciser la conjecture
et invite à tracer le segment [AM] pour préciser son rôle …
 |
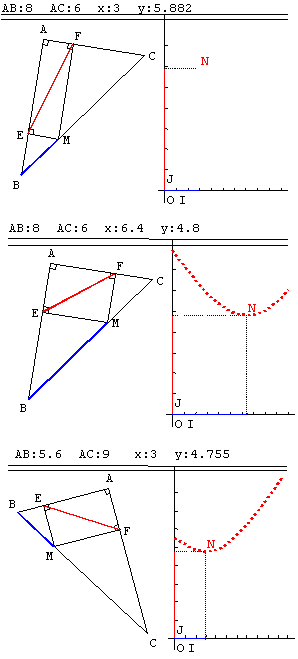 |
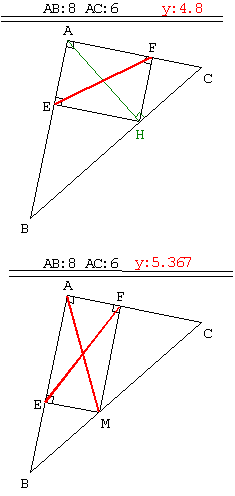
| Il semble que le
point H, pied de la hauteur issue de A, corresponde à la position recherchée
pour M …
7. Commande H :
Segment hauteur [AH].
Ce qui termine le travail de conjecture.
Vers la justification :
8. Commande R :
Surligne le rectangle AEMF.
Commande CTRL D :
Diagonale [AM].
Après avoir focalisé l’attention des élèves sur le rectangle
AEMF, le rôle de la diagonale [AM] émerge … Trouver la position de M qui
minimise AM (donc EF) et justifier ce résultat entre dans le domaine de
compétence d’un élève de Troisième (et même de Quatrième).
Ce travail fait l’objet de la partie II de la “ fiche
élève ”. |
 |




