Le cryptage RSA

4 avril 2001

Historique

En 1978, trois mathématiciens, Rivest, Shamir et Adleman, ont mis au point une méthode de cryptage à clé publique, procédé aujourd'hui largement utilisé pour assurer la sécurité des données sur Internet.

La méthode RSA (dont le nom est un acronyme formé des initiales de ses inventeurs) permet à chacun de coder un message à partir d'une clé publique mais n'autorise pas le décodage qui est conditionné à la connaissance d'une clé privée.

La sécurité de ce système de cryptage repose sur le fait qu'il est très facile de calculer, à l'aide d'un ordinateur ou d'une calculatrice symbolique, de très grands nombres premiers mais que la factorisation d'un très grand nombre prend un temps considérable sur les machines actuelles pour peu que les nombres premiers qui le compose soient suffisamment grands.

Mathématiquement, cette méthode repose sur un théorème d'Euler.

Soit p et q deux nombres premiers (des entiers naturels). Alors

a^{k(p-1)(q-1)+1} = a (mod pq)

Le nom de ce mathématicien célèbre a été crypté en suivant l'algorithme ci-dessous.

• chaque lettre est remplacée par son code ASCII.

  Espace-32	C - 67	F - 70	I - 73	L - 76	O - 79	R - 82	U - 85	X - 88
  A - 65	D - 68	G - 71	J - 74	M - 77	P - 80	S - 83	V - 86	Y - 89
  B - 66	E - 69	H - 72	K - 75	N - 78	Q - 81	T - 84	W - 87	Z - 90

• les nombres à deux chiffres ainsi obtenus sont regroupés deux par deux pour former des nombres à quatre chiffres.
• les résultats sont transformés par la fonction :
  

On obtient alors : 6690 / 5117 / 0199 / 4193 / 5976 / 4184

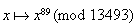
Quel est donc ce mathématicien ?

1. Factoriser le nombre 13493. On obtient ainsi les nombres premiers p et q.
2. Rechercher un entier x tel que 89x = k(p-1)(q-1). On pourra utiliser la table de valeur de la calculatrice.
3. Élever chacun des résultats à la puissance x.
4. Décoder à l'aide de la table ASCII.

Bientôt quelques indications !