On considère la suite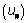 
définie pour
tout n appartenant à N*
par : 
.
Somme des termes d'une suite |
|
Projet d'activité créé lors
d'un stage |
|
1ère S – Terminale S
On considère la suite 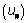définie pour
tout n appartenant à N*
par : .
TP en salle informatique
Phase expérimentale :
· Les élèves calculent à l’aide du tableur OpenOffice les premiers termes de la suite
· Il est difficile de conjecturer à l'aide des valeurs trouvées l'expression de la suite en fonction de n : l’idée est alors de construire le nuage de points
· On peut alors conjecturer qu’il est possible d’ajuster le nuage de points par une parabole
· Pour identifier la fonction f d’ajustement, on utilise SineQuaNon (ajustement polynomial d’une série statistique à deux variables)
Phase théorique :
· On vérifie par le calcul l'expression de f en résolvant un système 3x3 obtenu avec trois points choisis de manière judicieuse (à coordonnées entières)
· En Terminale les élèves démontrent par récurrence l'expression conjecturée.
On considère la suite définie pour
tout n appartenant à N*
par : .
1) Calculer à l'aide d'un tableur les quinze premiers termes de la suite , puis compléter
le tableau suivant :
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2) Utiliser le tableur pour faire apparaître la représentation graphique des points (n ; un) ;
3) a/ Conjecturer un type
de fonction dont la représentation graphique ajuste au mieux le nuage de
points.
b/ Utiliser le grapheur Sinequanon (menu : statistiques à deux variables è lissage polynomial) pour conjecturer
l'expression de la fonction.
c/ Déterminer par le calcul la fonction g définie sur R par 
dont
la représentation graphique passe par 3 points convenablement choisis du nuage.
Écrire ci-dessous le système et sa solution.
d/ Conjecturer l'expression de un en fonction de n.
4) Démontrer la conjecture précédente en utilisant un raisonnement par récurence.
