Le triangle de Sierpiński |
|
Projet d'activité créé lors
du stage tableur |
|
1e S
On considère un triangle équilatéral de côté 10 cm.
A chaque étape, on construit dans chaque triangle équilatéral non coloré, le triangle équilatéral coloré (en noir) ayant pour sommets les milieux des côtés. Les schémas suivants montrent les étapes 1 à 3.
On note pn et an le périmètre et l'aire de la surface colorée à l'étape n.
L'objectif est d'étudier le sens de variation et les limites éventuelles des deux suites (pn) et (an).
Phase de réflexion en classe entière :
Sans la fiche élève et sans le fichier tableur prévu, présentation du problème
et questionnement sur la façon d'obtenir les premiers termes de ces suites.
Réponses attendues ou questions pouvant être posées aux élèves :
A l'étape 1, ……. triangle est rajouté
A l'étape 2, …..... triangles sont rajoutés
A l'étape 3, …..... triangles sont rajoutés
On peut conjecturer que :
A l'étape n, …….. triangles sont rajoutés.
Le professeur demande ensuite aux élèves de :
- calculer l'aire du triangle initial ;
- calculer, à une étape donnée, le périmètre du triangle coloré en fonction du périmètre du triangle non coloré ;
- calculer, à une étape donnée, l'aire du triangle coloré en fonction de l'aire du triangle non coloré.
En
salle informatique :
Avec le fichier prévu et la fiche de questions, les élèves complètent le
tableau et émettent des conjectures.
Les démonstrations peuvent être terminées à la maison.
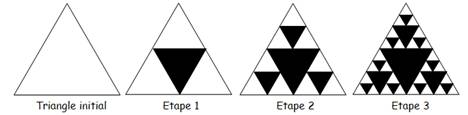
On considère un triangle équilatéral de côté 10 cm.
A chaque étape, on construit dans chaque triangle équilatéral non coloré, le triangle équilatéral coloré (en noir) ayant pour sommets les milieux des côtés. Les schémas suivants montrent les étapes 1 à 3.
On note pn et an le périmètre et l'aire de la surface colorée à l'étape n.
L'objectif est d'étudier le sens de variation et les limites éventuelles des deux suites (pn) et (an).
Première partie : Calcul des termes des suites (pn) et (an)
Ouvrir le fichier triangles_sierpinski.ods et compléter les colonnes par des formules :
· Entrer en colonne A les numéros des étapes.
· En colonne B, calculer le nombre de triangles colorés rajoutés à l'étape n.
· En colonne C, calculer le périmètre d'un triangle rajouté à l'étape n.
· En colonne D, calculer le périmètre de la surface colorée rajoutée à l'étape n.
· En colonne E, calculer le périmètre de la surface colorée à l'étape n.
· En colonne F, calculer l'aire d'un des triangles colorés rajoutés à l'étape n.
· En colonne G, calculer l'aire des triangles colorés rajoutés à l'étape n.
· En colonne H, calculer l'aire totale colorée à l'étape n.
Deuxième partie : Conjectures sur le sens de variation et les limites éventuelles des suites (pn) et (an)
· Quelle conjecture peut-on faire sur le sens de variations de la suite (an) ?
· Quelle conjecture peut-on faire sur le sens de variations de la suite (pn) ?
· Quelle est le périmètre de la surface colorée à l'étape 20 ?
· A partir de quelle valeur de n le périmètre pn est-t-il supérieur à 100 000 m ?
· A partir de quelle valeur de n le périmètre pn est-t-il supérieur à 4 000 000 m ?
· La suite (pn) admet-elle une limite ?
·
A partir de quelle valeur de n l'aire
de la surface colorée an est-elle située dans l'intervalle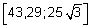 
?
·
A partir de quelle valeur de n
l'aire de la surface colorée an est-elle située dans
l'intervalle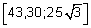 
?
· Quelle conjecture peut-on faire sur la limite de la suite (an) ?
Troisième partie : Mathématisation du problème
On note bn l'aire non colorée à l'étape n.
1)
Justifier que :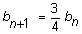 
pour tout n ≥ 1.
2) En déduire l'expression de bn en fonction de n.
3) En déduire l'expression de an en fonction de n.
4) Étudier le sens de variation de la suite (an) et calculer la limite de la suite (an).