Projet d'activité TICE

 

Niveau :

Première

Objectifs

Résoudre un problème « concret ».

La partie algorithmique peut être traitée de différentes manières selon l'objectif recherché par l'enseignant ; la fiche élève propose deux approches différentes.

 

Prérequis :

• Utilisation des notions d’algorithmique et du mode de programmation de Xcas.

Enoncé :

 

Dans un groupe de n individus choisis au hasard et tous nés lors d'une année de 365 jours, la probabilité que les n anniversaires tombent à des jours tous différents est notée p_n.

 

-       On cherche à calculer p_n pour certaines valeurs de n puis à déterminer une relation entre p_n+1 et p_n.

 

-       On se donne un nombre positif q inférieur à 1 et on cherche, avec un algorithme, à partir de combien d'individus p_n est inférieure à q.

 

Organisation pratique :

 

Travail autonome en salle informatique

 

Fichiers disponibles

 

•  La fiche élève 1 au format pdf (fichier pdf)
•  La fiche élève 2 au format pdf
•  Les fichiers Xcas compressés (fichier zip)

 

Les fiches élèves

 

Fiche élève 1

 

Dans un groupe de n individus choisis au hasard et tous nés lors d'une année de 365 jours, la probabilité que les n anniversaires tombent à des jours tous différents est notée .

 

1)      Si , que vaut  ?

 

2)      Cas où  : calculer .

 

3)      Cas où  : expliquer pourquoi .

 

4)      Cas où  : calculer .

 

5)      Cas général : expliquer pourquoi pour tout k compris entre 1 et 364, .

 

6)      Compléter la phrase : « Plus n est grand, plus  est…………….. ».

 

 

7)      On se donne un nombre positif q inférieur à 1 et on cherche à partir de combien d'individus  est inférieure à q. Compléter sur papier l'algorithme ci-dessous :

 

 

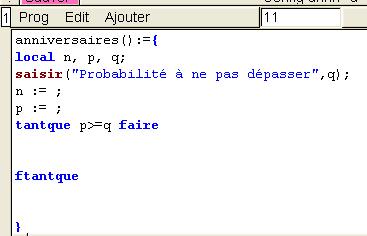
8)      Dans une session Xcas, coder l'algorithme précédent.

 

9)      Utiliser l'algorithme précédent pour déterminer à partir de combien d'individus on a moins de 50% de chances qu'ils soient tous nés un jour différent de l'année.

 

10)  Utiliser l'algorithme précédent pour savoir à partir de combien d'individus la probabilité d'en avoir au moins deux nés le même jour est plus grande que 0,9.

 

Fiche élève 2

 

Dans un groupe de n individus choisis au hasard et tous nés lors d'une année de 365 jours, la probabilité que les n anniversaires tombent à des jours tous différents est notée .

 

1)      Si , que vaut  ?

 

2)      Cas où  : calculer .

 

3)      Cas où  : expliquer pourquoi .

 

4)      Cas où  : calculer .

 

5)      Cas général : expliquer pourquoi pour tout k compris entre 1 et 364, .

 

6)      Compléter la phrase : « Plus n est grand, plus  est…………….. ».

 

 

7)      Compléter sur papier l'algorithme ci-dessous qui permet de calculer  pour un n donné :

 

 

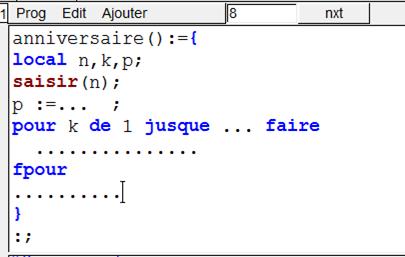
8)      Dans une session Xcas, coder l'algorithme précédent.

 

9)      Utiliser l'algorithme précédent ou en créer un nouveau pour répondre aux questions suivantes :
a) déterminer à partir de combien d'individus on a moins de 50% de chances qu'ils soient tous nés un jour différent de l'année.                         
b) à partir de combien d'individus la probabilité d'en avoir au moins deux nés le même jour est plus grande que 0,9.