Six exercices sur les graphes |
|
| Équipe académique mathématiques |
|
1. Recherche d'une chaîne eulérienne
4. Algorithme de recherche d'une plus courte chaîne
5. Graphes étiquetés - automates
6. Graphe probabiliste - matrice de transition.
Problème
| Sept ponts enjambent la Pregel, reliant quatre quartiers de la ville. Les habitants se demandent s’il existe un trajet leur permettant d’emprunter une seule fois tous les ponts. Euler modélise le problème et ouvre ainsi une nouvelle théorie. |
|
|
|
Les quartiers sont les sommets du graphe, les ponts les arêtes. Il y a quatre sommets (l'ordre du graphe est 4), au sommet A arrivent trois arêtes (le degré de A est 3). Le problème posé induit deux questions : existe-t-il un trajet partant d'un point donné, passant par toutes les arêtes une et une seule fois (chaîne eulérienne) ? Ou bien existe-t-il une chaîne eulérienne revenant au point de départ (cycle eulérien) ? |
Le théorème d'Euler énonce qu'un graphe non orienté admet une chaîne eulérienne si et seulement si il est connexe et admet zéros ou deux sommets impairs. Si tous les sommets sont pairs, il s’agit de cycle eulérien.
À Königsberg, rebaptisée depuis Kaliningrad, il y a deux nouveaux ponts, l'un entre B et C et l'autre entre B et A. Y a-t-il une chaîne eulérienne ?
Où faudrait-il construire un autre pont pour obtenir un cycle eulérien ?
D’après « Réciproques » n°16 de décembre 2001
Réponse
|
|
Le théorème d’Euler répond à tous les exercices de recherche de chemin dans un graphe ; dans celui ci-contre, il y a quatre sommets de degrés impairs donc il n’y aura ni chemin eulérien, ni cycle eulérien. |
| Si on rajoute une arête entre B et C et une autre entre B et A, il y a maintenant deux sommets de degré pair (A et C) et deux de degré impair (B et D) : ce graphe admet donc une chaîne eulérienne qui doit partir de B pour arriver à D (par exemple : B–A–B–C–A–D–B–D–C–D) ou partir de D pour arriver à B (D–A–B–C–D–B–A–C–D–B). |
|
|
|
Pour obtenir un cycle eulérien, il faudrait que tous les sommets soient de degré pair ; il suffit donc de relier entre eux les deux sommets de degré impair du graphe précédent : on construit donc une nouvelle arête (c’est-à-dire un nouveau pont) entre B et D. On aurait pu supprimer une arête entre B et D ce qui aurait rendu tous les sommets pairs et donc permis un cycle eulérien. |
Problème
Une école doit faire passer des tests écrits à quatre élèves : Adrien, Sophie, Charlotte et Matthieu. Sept disciplines sont concernées : les mathématiques, la physique, la biologie, le français, l'anglais, l'espagnol et l’histoire.
Adrien doit passer les mathématiques, la physique et l'anglais, Sophie les mathématiques, la biologie et le français, Charlotte les mathématiques, l'anglais et l'espagnol et Matthieu la physique, le français et l'histoire.
Quel est le nombre minimal de plages horaires à prévoir pour qu'aucun élève n'ait à passer deux tests simultanément ?
|
|
On peut modéliser la situation par le graphe représenté ci-contre ; les sommets représentent les disciplines, les arêtes relient les disciplines dont les tests ne peuvent avoir lieu simultanément. Les plages horaires sont représentées par des formes géométriques (ou par des couleurs). On attribue à chaque sommet une forme, deux sommets adjacents ne pouvant avoir la même. Le sous-graphe complet M, A, E (tous les sommets sont adjacents) nécessite trois formes. Le dessin prouve que trois sont suffisantes pour le graphe. Ainsi le nombre chromatique du graphe est trois. |
Si Adrien doit aussi passer le test d’histoire, le nombre chromatique devient supérieur ou égal à quatre. Un dessin prouve qu'il est de quatre.
Extrait de « Réciproques » n°16 de décembre 2001
Remarque
Problème classique de coloration de graphe que l’on rencontre dans des cas d’incompatibilité :
# on veut regrouper des animaux dans un minimum de cages mais certains d’entre eux sont des prédateurs d’autres ;
# on veut constituer une tablée mais certains convives ne veulent pas se trouver à côté de certains autres ;
# on ne veut pas que, dans un carrefour, certaines files de voitures en croisent certaines autres...
III - Des goûts et des couleurs
![]()
Problème
On ne sait pas toujours trouver le nombre minimum de couleurs pouvant colorer un graphe (le « nombre chromatique » du graphe) ; des algorithmes existent qui donnent un nombre de couleurs possible, ce nombre n’étant pas forcément le plus petit.
Voici un algorithme de coloration de graphes.
On range les sommets dans l’ordre décroissant de leurs degrés : s1, s2, s3 … sn.
On colorie ces sommets dans l’ordre précédemment défini avec pour règle de donner à chaque sommet la couleur la plus petite (on suppose les couleurs numérotées dans l’ordre croissant), en fonction des sommets voisins qui sont déjà colorés.
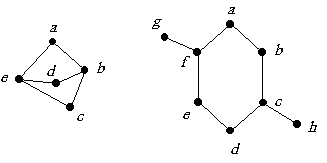
| Appliquer cet algorithme aux deux graphes représentés ci-contre.
Comparer, pour chaque graphe, le nombre de couleurs obtenues avec son nombre chromatique. |
 |
Réponse
|
|
En suivant l’algorithme proposé dans le texte de l’exercice, voici le tableau de coloration pour le graphe ci-contre :
|
On attribue au premier sommet b la couleur n°1 ; puis on regarde si on peut attribuer la couleur n°1 au deuxième sommet e : comme les sommets b et e ne sont pas reliés, on peut prendre la même couleur. On regarde si on peut attribuer au troisième sommet a la couleur n°1 : c’est non puisque a et b sont reliés entre eux. On attribue donc une autre couleur n°2 au sommet a. Et on se pose les mêmes questions pour les sommets c et d : on voit qu’on ne peut les colorier avec la couleur n°1 mais que l’on peut les colorier avec la n°2.
L’algorithme proposé donne donc deux couleurs pour le graphe ; on ne peut pas en avoir moins : deux est donc le nombre chromatique de ce graphe.
| On applique le même algorithme à cet autre graphe :
L’algorithme donne un nombre de couleurs de 3 alors qu’on peut se rendre compte rapidement que deux suffisent : couleur 1 pour les sommets c, a, g et e ; couleur 2 pour les sommets b, f, d et h. |
|
L’algorithme proposé dans cet exercice donne UNE coloration de n’importe quel graphe mais ne donne pas le nombre chromatique du graphe ; en fait, il n’existe pas d’algorithme permettant de trouver le nombre chromatique d’un graphe quelconque.
Problème
Un graphe peut représenter un chemin qu’un voyageur de commerce aurait à parcourir ; des contraintes existent : kilométrage entre deux villes, coût des péages d’autoroutes… Il s’agit de trouver un chemin entre différents sommets de coût minimum : on dira qu’il s’agit de chercher un « plus court chemin ».
L’algorithme suivant permet de trouver le plus court chemin entre un sommet d’un graphe et chacun des autres.
Les données sont : un graphe G et un sommet de départ s. On associe à chaque sommet x le coût du meilleur chemin connu appelé poids(x). On mémorise également, pour chaque sommet, le voisin par lequel on « arrive » pour réaliser le meilleur chemin connu. Soit S l’ensemble de tous les sommets et P l’ensemble des sommets optimaux (c’est-à-dire les sommets affectés du coût minimal).
Initialisation
poids(s) ¬ 0
poids(x) ¬ +¥ pour x ¹ s
P ¬ Æ
début
tant que P ¹ S
choisir un sommet x Ï P de poids minimum
P ¬ P È {x}
pour tout voisin y de x n’appartenant pas à P
si poids(x) + valeur(x y) < poids(y)
alors poids(y) ¬ poids(x) + valeur(x y)
mémoriser en y que l’on vient de x
fin si
fin pour tout
fin tant que
fin
|
|
Faire tourner cet algorithme sur le graphe ci-contre pour trouver tous les chemins minimaux partant de s. |
Voir aussi : http://www.jura.ch/lcp/cours/dm/dijkstra/index.html
Réponse
| Voici la suite des résultats obtenus en faisant tourner l’algorithme donné dans l’exercice (algorithme de Dijkstra) sur le graphe ci-contre :
|
|
D’où les chemins :
de s vers d direct de coût 2 ;
de s vers c de s vers d puis de d vers c (total 4) ;
de s vers b de s vers d puis de d vers c puis de c vers b (total 6) ;
de s vers a de s vers d puis de d vers c puis de c vers a (total 5).
On peut trouver à l’adresse http://www.jura.ch/lcp/cours/dm/dijkstra/index.html une animation Java qui visualise l’algorithme de Dijkstra.
Problème
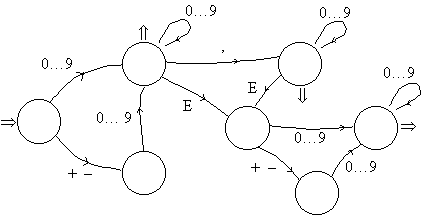
| Le graphe ci-contre représente un automate qui permet de reconnaître un entier naturel dont l’écriture est normalisée (ne commençant pas par un 0, s’il est non nul) : On entre un nombre entier par la gauche et selon le premier chiffre on se dirige vers la branche du bas (si c’est un zéro) ou celle du haut (sinon). Sur le même principe, représenter un automate qui reconnaît une entrée numérique dans un tableur (par exemple : 12,3 ; 08 ; –15 ; 5E12 ou 14E–3). |
|
| Autre exemple. Dans un alphabet ne comportant que deux lettres a et b, l’automate ci-contre reconnaît les mots ne contenant pas la lettre a. |
|
Représenter un automate qui reconnaisse les mots ne comportant pas la séquence ab, puis un qui reconnaisse les mots ne comportant pas la séquence aba, etc.
Solution
Voici un automate qui permet de reconnaître une entrée numérique dans un tableur :
Dans un alphabet ne comportant que deux lettres a et b, voici un automate reconnaissant les mots
| ne comportant pas la séquence ab : |
|
| ne comportant pas la séquence aba : |
|
VI - Des matrices et des graphes
![]()
Problème
Sur un marché, deux produits A et B sont en concurrence (par exemple deux lessives).
On suppose que d'une année à l'autre, 60 % de la clientèle reste fidèle à A tandis que 30 % de la clientèle de B passe à A. Il n'y a pas de fuite de clientèle vers d'autres produits concurrents, et il n'y a pas abandon de consommation de ces produits.
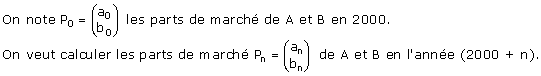
1) Calculer P1, puis P2.
2) a) Démontrer que Pn+1= M Pn, où M est une matrice carrée d'ordre 2 que l'on précisera.
b) En déduire que Pn = Mn P0.
3) Vérifier que M2 – M = 0,3 (M ‑ I) , où I désigne la matrice unité d'ordre 2.
En déduire que : Mn - Mn-1 = (0,3)n-1 (M - I).
4) Calculer Mn et en déduire Pn.
Tiré du Bréal 1re ES – N° 47 page 241
Réponse
| Le graphe probabiliste associé est : |
|
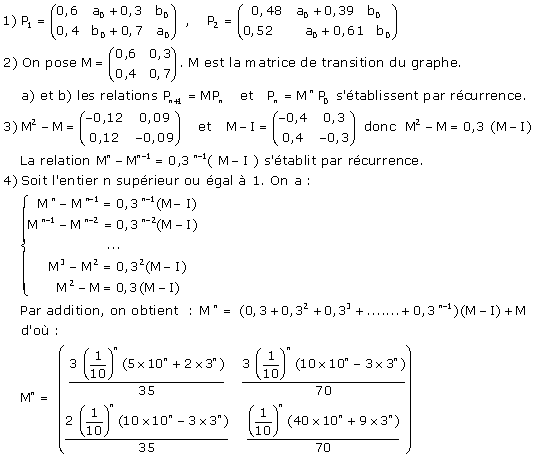 .
.