« L'acquisition de techniques de calcul faisant appel à des lettres est un des points délicats de l'enseignement des mathématiques au collège » (document d'accompagnement du cycle central).

Nous avons vu, à travers les diverses activités de la journée, combien l'enseignement de l'algèbre dans les classes de collège demande au professeur de faire un travail très progressif et renouvelé au fil des classes sur la lettre et l'égalité, afin d'aider les élèves à bien en distinguer les différents statuts.

Les lettres sont en effet utilisées avec différents  statuts :

—  de façon « expressive » pour signifier des grandeurs (comme dans la formule de l'aire du rectangle) ;

—  pour désigner des inconnues (dans les problèmes de mise en équation) ;

—  pour nommer les variables (dans le langage des fonctions) ;

—  comme valeurs indéterminées (dans les identités remarquables).

Le signe " = " prend, lui aussi, différents statuts :

—  un sens dynamique ( lié au "EXE" de la calculatrice) lorsqu'on effectue des calculs ;

—  le signe « égale » qui lie deux écritures distinctes d'un même objet (12 + 5 = 8 + 3 + 6) ;

—  l'égalité dans les équations (qui est à interpréter comme « pour quels nombres l'égalité est-elle vraie ? ») ;

L'utilisation des propriétés de l'égalité, par exemple la transitivité, ajoutera  une difficulté supplémentaire :

—  l'identité (une identité est une égalité qui est vraie pour tous les nombres).

Les programmes ont pris en compte ces difficultés liées aux différents statuts de la lettre et de l'égalité. Ils prônent une introduction très progressive des différents sens de la lettre avec un grand travail d'approche en 6^e et en 5^e.

En sixième

On trouve dans le programme deux chapitres totalement distincts :

—  Initiation à la résolution d'équations

—  Initiation aux écritures littérales

1. Dans le chapitre « Initiation à la résolution d'équations », on pourra :

—  faire un schéma pour traduire une équation

Jean mesure 15 cm de plus que Pierre ; or Jean mesure 1 m 20 ; quelle est la taille de Pierre ?

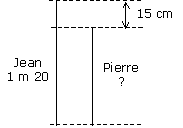
—  essayer de compléter des égalités à trous en utilisant uniquement le sens de l'opération :

15 + ? = 120

—  faire reformuler les phrases :

la somme de 15 et du nombre cherché est 120 ; si j'additionne 15 à ce nombre, je trouve 120 ; quel nombre dois-je ajouter à 15 pour trouver 120, etc.

On veillera à habituer l'élève à passer d'un registre à l'autre.

Pour la résolution à proprement parler, la désignation de l'inconnue par une lettre n'est pas nécessaire dans ces activités ; aucune technique n'étant installée, on procède en faisant référence au sens de l'opération.

On rencontrera cinq types d'équations :

3 + ‘ = 21    ‘ - 23 = 14   62 - ‘ = 25   3 x ‘ = 2,1    et éventuellement  ‘ : 24 = 25

2. Dans le chapitre « Initiation aux écritures littérales », on appliquera une formule littérale dans des situations familières aux élèves.

On pourra essayer de schématiser des calculs en utilisant des lettres qui, à chaque usage, seront remplacées par des valeurs numériques (par exemple, réaliser un petit programme : je prends un nombre, je le multiplie par 3, puis j'ajoute 1 ; appliquer ensuite ce programme à 8, puis à 5,... , puis à _x ) en faisant prendre conscience aux élèves de l'intérêt « économique » de cette schématisation (on doit effectuer les calculs : 15 x 3 + 7 ; 15 x 9 + 7 ; 15 x 0,6 + 7 ; 15 x 11 + 7 ; etc. Comment peut-on donner plus rapidement la consigne ?)

Il faut dans cette classe travailler le sens de l'égalité

(l'élève écrit : 5 + 3 + 8 + 2 = 8 + 8 = 16 + 2 = 18 ; le même aura du mal à admettre que :  8 + 7 = 3 + 12, alors qu'il maîtrise correctement l'addition des entiers naturels. Il est nécessaire à ce stade de clarifier le sens du signe « égal » qui a dans ces exemples un sens de relation, et qui n'est pas le signal de l'exécution d'une procédure ; il faut donc les habituer  à écrire  2 + 1/3 = 1 + 4/3 ; 15 = 5 + 10. et pas seulement  5 + 10 = 15)

En cinquième

Contrairement à ce qui est proposé en classe de sixième, les thèmes « Calcul littéral » et « Initiation à la résolution d'équations » sont étroitement imbriqués, ce qui implique une mise au point indispensable des différents rôles du signe « égal ».

—  C'est la première fois que l'élève rencontre une identité : la lettre y figure en tant qu'indéterminée et l'égalité est toujours vraie (la première de ces égalités, exigible en cinquième, est l'égalité liée à la distributivité de la multiplication par rapport à l'addition)

—  Le chapitre "Tester une égalité, une inégalité comportant un ou deux nombres indéterminés", qui n'existait pas dans les anciens programmes, est une étape importante dans l'acquisition du sens d'une équation. En présentant des égalités vues comme des assertions dont la véracité est à examiner (exemple : tester l'égalité 4y + 24 = 104 pour des valeurs numériques données dont l'une va convenir), on donne du sens à la notion d'équation.

C'est l'occasion de faire travailler les notions de propriétés et de contre-exemple : si l'égalité est une identité, il faut le démontrer ; si on trouve un contre-exemple, l'identité n'est pas vraie.

—  En 5^e, on remplace l'inconnue par la lettre dans les équations mais, pour la résolution, on s'appuie uniquement sur le sens des opérations.

"Aucune méthode de résolution n'est donnée de manière à éviter l'écueil connu d'apprentissages aboutissant à la mise en oeuvre d'algorithmes dépourvus de sens" (commentaire du programme officiel)

En fin de cinquième, l'élève doit avoir rencontré les différents statuts de la lettre et de l'égalité. Il faut donc accorder du temps à tous ces chapitres et à toutes ces activités qui donneront du sens à ces statuts.

En quatrième et en troisième

—  on découvre d'autres identités (double distributivité, identités remarquables) ;

—  on met en place les algorithmes de résolutions d'équations et de systèmes d'équations ;

—  en commençant à introduire la notion de fonction, et avec elle la notion de variable, on ouvre un autre champ qui occupera une place importante au lycée. Jusqu'alors, la notion de fonction n'a été utilisée que de façon implicite par le biais des expressions « en fonction de » ou « est fonction de », et ce, dès la sixième.

La notation fonctionnelle amène à utiliser la lettre avec une nouvelle signification. On utilise la notation f(x) seulement pour des valeurs particulières de la variable (f(1), f(5), etc.) On évite l'écriture f(x). La difficulté à comprendre ce nouveau statut de la lettre ainsi que le nouveau sens des parenthèses justifie le fait que la notion d'équation de droite ne soit pas abordée au collège.