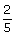 du
téléphone, Jean donne
du
téléphone, Jean donne 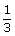 du
prix et Christophe 40 euros.
du
prix et Christophe 40 euros.La mise en équation de problèmes |
|
Équipe académique Mathématiques |
|
Les exercices qui suivent portent tous sur la mise en équation de problèmes. — A quel niveau peut-on donner chacun de ces exercices ? — Quelle méthode de résolution utilise-t-on ? — Cet exercice est-il pertinent pour montrer le recours à l'algèbre dans la résolution du problème ? |
1- Les économies de Pierre sont trois fois plus importantes que celles de son frère Benoît. Leur sour Anne a 12 euros de plus que Pierre. A eux trois, ils ont 425 euros.
Calculer le montant des économies de chacun.
2- Un vase a la forme d'un pavé droit de 12 cm de longueur et 9 cm de largeur. On le remplit de 2,7 L d'eau.
Quelle est la hauteur d'eau ?
3- Jean, Christophe et Aline offrent un téléphone à leurs parents.
Aline paie les 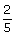 du
téléphone, Jean donne
du
téléphone, Jean donne 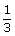 du
prix et Christophe 40 euros.
du
prix et Christophe 40 euros.
Quel est le prix du téléphone ?
4- Le périmètre d'un rectangle est de 168 m. La largeur représente
les 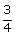 de
la longueur.
de
la longueur.
Quelles sont les dimensions du rectangle ?
5- Si on divise un nombre décimal par 1,25, on trouve 4,28.
Quel est ce nombre ?
6- Si on additionne le même nombre entier au numérateur et au dénominateur
de 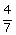 ,
on obtient
,
on obtient 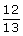 .
.
Quel est ce nombre ?
7- La somme de quatre multiples de 7 consécutifs est égale à 238.
Déterminer ces quatre nombres.
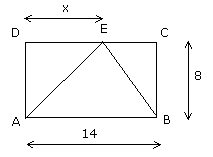
8- ABCD étant un rectangle. 1) Comment choisir x pour que les aires des triangles ADE et BCE soient égales ? 2) Comment choisir x pour que l'aire du triangle ADE soit égale au tiers de l'aire du triangle BCE? 3) Comment choisir x pour que la somme des aires des triangles ADE et BCE soit égale à l'aire du triangle ABE ? |
 |
|
|
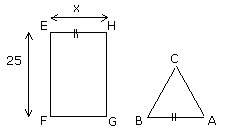
9- Déterminer x pour que le périmètre du triangle équilatéral ABC soit le tiers du périmètre du rectangle EFHG. |
 |
10- Un père de 42 ans a une fille de 12 ans.
Dans combien d'années l'âge du père sera-t-il le triple de l'âge de sa fille ?
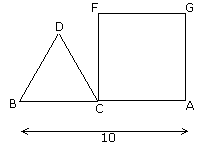
11- Le carré ACFG et le triangle équilatéral BDC ont le même périmètre. Quelle est la mesure d'un côté du triangle ? |
 |
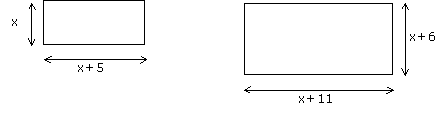
12- Voici deux rectangles dont les dimensions sont indiquées en cm. On sait que l'aire du plus grand est supérieure de 100 cm2 à celle du petit.
Calculer les dimensions des deux rectangles.
13- J'ai trois fois plus de billes que Jean et Pierre en a cinq fois plus. Si j'en avais 10 de plus et Pierre 8 de moins, nous en aurions tous les deux autant.
Combien chacun de nous trois a-t-il de billes ?
14- Jean et Jacques ont donné le même somme. A l'un, on a rendu 1,2 euros et donné 4 cahiers. A l'autre, on a rendu 3,5 euros et donné deux cahiers.
Combien coûte un cahier ?
15- Déterminer x pour que les deux solides ci-dessous aient le même volume.
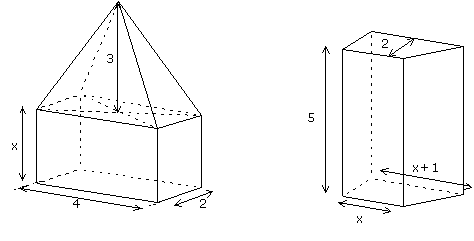
Le premier solide est formé d'un pavé de longueur 4, de largeur 2 de hauteur x surmonté d'une pyramide de hauteur 3.
Le deuxième est un prisme droit de hauteur 5 dont la base est un trapèze de bases x et x+1 et de hauteur 2.