Prolongement |
|
Équipe académique Mathématiques |
|
Il serait toutefois dommage de ne considérer l'algèbre que comme un outil permettant de résoudre des problèmes où l'arithmétique peut être mise en défaut.
Par exemple, on peut envisager de présenter l'algèbre de façon pertinente à partir de problèmes de géométrie ou des problèmes conduisant à prouver des propriétés numériques (« arithmétiques » au sens de calcul sur les nombres entiers).
Exemples
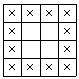
1. Problème de géométrie : choix d'une situation Le problème consiste à établir une formule permettant de calculer le nombre de carreaux marqués d'une croix d'une figure construite sur le modèle ci-dessus, quel que soit le nombre de carreaux sur le côté du carré. |
|
2. L'arithmétique au sens habituel du terme :
— démontrer que la somme d'un nombre pair et d'un nombre impair est un nombre impair
— démontrer les propriétés suivantes :
si un nombre entier est pair, alors son carré est pair
si un nombre entier est impair, alors son carré est impair
— démontrer que la différence des carrés de deux nombres entiers consécutifs est impaire
Et tant d'autres..
