Apprentissages numériques de l’école au collège : enjeux, difficultés, évolutions |
| Intervention de Roland Charnay, |
1 Les nombres et leurs désignations
Je situerai aujourd’hui plutôt mon intervention à l’articulation de l’école et du collège, dans le but de préciser la responsabilité de l’école et du collège (notamment des premières années du collège) vis-à-vis des apprentissages numériques à partir de trois réflexions :
 les
enjeux de ces apprentissages sur l’ensemble de la scolarité obligatoire ;
les
enjeux de ces apprentissages sur l’ensemble de la scolarité obligatoire ;
 les
connaissances attendues des élèves au terme de l’école primaire tels que les
définissent les programmes actuels ;
les
connaissances attendues des élèves au terme de l’école primaire tels que les
définissent les programmes actuels ;
 les
difficultés constatées, en particulier à partir de l’analyse des évaluations
à l’entrée en Sixième.
les
difficultés constatées, en particulier à partir de l’analyse des évaluations
à l’entrée en Sixième.
Le champ recouvert par l’intitulé « Apprentissages numériques » est très vaste. La proposition actuelle concernant les programmes de collège adopte un découpage très voisin de celui de l’école primaire de façon à mieux faire apparaître les continuités, à les rendre plus lisibles pour les enseignants.
| Cycle 3 de l’école primaire |
Collège |
| Exploitation de données numériques |
Organisation et gestion de données, fonctions |
| Connaissance des nombres entiers naturels |
Nombres et calcul |
| Connaissance des fractions simples et des nombres décimaux |
|
| Calcul |
|
| Espace et géométrie |
Géométrie |
| Grandeurs et mesure |
Grandeurs et mesure |
Tous les domaines, même la géométrie, sont concernés par l’utilisation des nombres.
Je n’aborderai pas tous ces domaines et me limiterai à trois points qui ne sont évidemment pas indépendants les uns des autres :
1. L’apprentissage des nombres et de leurs désignations
2. L’apprentissage du calcul
3. La résolution de problèmes impliquant les nombres, avec un intérêt plus particulier pour la proportionnalité.
1 Les nombres et leurs désignations
![]()
À l’issue du collège, ont été travaillés les entiers, les décimaux et les rationnels. Le travail sur les racines carrées entrepris en 3e permet une toute première approche des nombres réels (non rationnels).
Si on regarde cet apprentissage à travers la problématique de l’articulation entre l’école et le collège, on peut dresser le tableau suivant.
 Selon
les programmes, les connaissances relatives à la numération décimale et à l’ordre
sur ces nombres sont des objectifs de l’école primaire, ce qu’enregistre d’ailleurs
le programme de Sixième. Il faut ajouter une première approche de l’arithmétique
(connaissance de relations entre nombres d’usages courants inférieurs à 100
et reconnaissance des multiples de 2, 5 et 10).
Selon
les programmes, les connaissances relatives à la numération décimale et à l’ordre
sur ces nombres sont des objectifs de l’école primaire, ce qu’enregistre d’ailleurs
le programme de Sixième. Il faut ajouter une première approche de l’arithmétique
(connaissance de relations entre nombres d’usages courants inférieurs à 100
et reconnaissance des multiples de 2, 5 et 10).
 Ces
connaissances ne font pratiquement l’objet d’aucune évaluation spécifique à
l’entrée en Sixième, en particulier pour ce qui concerne la signification des
écritures chiffrées et la valeur positionnelle des chiffres dans l’écriture
d’un nombre entier.
Ces
connaissances ne font pratiquement l’objet d’aucune évaluation spécifique à
l’entrée en Sixième, en particulier pour ce qui concerne la signification des
écritures chiffrées et la valeur positionnelle des chiffres dans l’écriture
d’un nombre entier.
 Deux
résultats cependant :
Deux
résultats cependant :
 La seule
question posée en 2000 sur la relation entre dizaines et unités laisse supposer
que la maîtrise de la numération en base dix est loin d’être assurée pour tous
les élèves à l’entrée en Sixième, ce qui peut expliquer d’autres difficultés
avec les nombres décimaux.
La seule
question posée en 2000 sur la relation entre dizaines et unités laisse supposer
que la maîtrise de la numération en base dix est loin d’être assurée pour tous
les élèves à l’entrée en Sixième, ce qui peut expliquer d’autres difficultés
avec les nombres décimaux.
Complète l’égalité 25 dizaines = …… unités n’est réussi que par 54 % des élèves
 La relation
entre désignation orale et désignation chiffrée est relativement bien acquise
(80 % à 90 % de réussite, selon la taille des nombres, mais l’écriture en chiffres
de trois cent quatre pose encore difficulté pour 10 % des élèves, après
quatre années de travail)
La relation
entre désignation orale et désignation chiffrée est relativement bien acquise
(80 % à 90 % de réussite, selon la taille des nombres, mais l’écriture en chiffres
de trois cent quatre pose encore difficulté pour 10 % des élèves, après
quatre années de travail)
 Selon
les programmes, les connaissances relatives à la numération décimale et à l’ordre
sur ces nombres sont également des objectifs de l’école primaire, le programme
de Sixième proposant d’en reprendre l’étude de façon plus importante que pour
les entiers.
Selon
les programmes, les connaissances relatives à la numération décimale et à l’ordre
sur ces nombres sont également des objectifs de l’école primaire, le programme
de Sixième proposant d’en reprendre l’étude de façon plus importante que pour
les entiers.
 Je
n’insisterai pas sur les difficultés constatées à l’entrée en Sixième, bien
connues et persistantes, et qui montrent que selon les exercices entre un quart
et la moitié des élèves rencontrent des difficultés aussi bien sur la compréhension
des écritures à virgule que sur les questions relatives à l’ordre.
Je
n’insisterai pas sur les difficultés constatées à l’entrée en Sixième, bien
connues et persistantes, et qui montrent que selon les exercices entre un quart
et la moitié des élèves rencontrent des difficultés aussi bien sur la compréhension
des écritures à virgule que sur les questions relatives à l’ordre.
 En
observant également les manuels scolaires deux conclusions complémentaires
peuvent être tirées :
En
observant également les manuels scolaires deux conclusions complémentaires
peuvent être tirées :
 du
côté de l’école primaire, le travail sur la compréhension des écritures décimales
(valeur des chiffres en fonction de leur position, relations entre unités de
rangs différents) est insuffisant et laisse trop rapidement la place à la mise
en place de techniques ou de questions formelles (repérage du chiffre des dizaines
et de celui des unités, par exemple) ;
du
côté de l’école primaire, le travail sur la compréhension des écritures décimales
(valeur des chiffres en fonction de leur position, relations entre unités de
rangs différents) est insuffisant et laisse trop rapidement la place à la mise
en place de techniques ou de questions formelles (repérage du chiffre des dizaines
et de celui des unités, par exemple) ;
 du
côté du collège, une reprise est nécessaire, sans refaire ce qui a été fait
à l’école primaire, mais en sollicitant en permanence la compréhension des écritures
décimales… et donc en évitant d’aller trop rapidement vers l’utilisation de
techniques non justifiées.
du
côté du collège, une reprise est nécessaire, sans refaire ce qui a été fait
à l’école primaire, mais en sollicitant en permanence la compréhension des écritures
décimales… et donc en évitant d’aller trop rapidement vers l’utilisation de
techniques non justifiées.
Ici, les objectifs sont beaucoup plus contrastés entre l’école et le collège.
 Les
programmes de l’école primaire proposent une approche limitée des fractions,
en se bornant à ce qui est nécessaire à la compréhension des nombres décimaux
(fractions de dénominateur simple et fractions décimales).
Les
programmes de l’école primaire proposent une approche limitée des fractions,
en se bornant à ce qui est nécessaire à la compréhension des nombres décimaux
(fractions de dénominateur simple et fractions décimales).
 les
fractions sont étudiées avec une seule signification :
les
fractions sont étudiées avec une seule signification :
5/3 c’est 5 fois 1/3 (5 fois la part obtenue en partageant l’unité en 3)
 à
partir de là, sont travaillées, par le biais du raisonnement, sans mise au point
de techniques :
à
partir de là, sont travaillées, par le biais du raisonnement, sans mise au point
de techniques :
- la relation avec 1 : 3/3 c’est 1, donc 5/3 est supérieur à 1 (rôle important de l’oral et des images mentales issues des manipulations préalables) ;
- la décomposition en nombre entier et fraction inférieure à 1 : 19/3 c’est 6 fois 3/3 plus 1/3, donc 6 + 1/3.
 Ces
connaissances sont peu évaluées à l’entrée en Sixième
Ces
connaissances sont peu évaluées à l’entrée en Sixième
 Alors
qu’elle occupe une place limitée à l’école primaire, l’écriture fractionnaire
va prendre une place centrale au collège : c’est un des outils essentiels
pour le traitement de nombreux problèmes, comme on le verra pour la proportionnalité
et comme on pourrait le montrer pour les grandeurs quotients. Plusieurs questions
se posent aux élèves et donc aux enseignants :
Alors
qu’elle occupe une place limitée à l’école primaire, l’écriture fractionnaire
va prendre une place centrale au collège : c’est un des outils essentiels
pour le traitement de nombreux problèmes, comme on le verra pour la proportionnalité
et comme on pourrait le montrer pour les grandeurs quotients. Plusieurs questions
se posent aux élèves et donc aux enseignants :
 L’écriture
fractionnaire prend une nouvelle signification, celle de quotient : 7/3
c’est le tiers de 7.
L’écriture
fractionnaire prend une nouvelle signification, celle de quotient : 7/3
c’est le tiers de 7.
 Il
faut donc que les élèves aient conscience de ces deux significations, tout en
s’assurant de leur équivalence : 7 fois le tiers de 1 c’est pareil que
le tiers de 7 (trop souvent cette équivalence est passée sous silence, n’est
pas travaillée et les deux conceptions cohabitent mal) [i] .
Il
faut donc que les élèves aient conscience de ces deux significations, tout en
s’assurant de leur équivalence : 7 fois le tiers de 1 c’est pareil que
le tiers de 7 (trop souvent cette équivalence est passée sous silence, n’est
pas travaillée et les deux conceptions cohabitent mal) [i] .
 Cette
écriture représente un nombre… et non un calcul à effectuer. L’élève fait un
pas important vers l’idée de nombre lorsqu’il accepte cela, comme ce sera également
le cas avec les nombres relatifs, puis avec les radicaux. L’usage excessif des
calculatrices qui incite à tout ramener à des « nombres en ligne »
n’y aide pas.
Cette
écriture représente un nombre… et non un calcul à effectuer. L’élève fait un
pas important vers l’idée de nombre lorsqu’il accepte cela, comme ce sera également
le cas avec les nombres relatifs, puis avec les radicaux. L’usage excessif des
calculatrices qui incite à tout ramener à des « nombres en ligne »
n’y aide pas.
 Elle
nécessite le passage à une conception plus théorique : au cycle 3, la fraction
est reliée au fractionnement effectif d’une grandeur ; en sixième 7/3 est
le nombre qui multiplié par 3 donne 7 – ce passage du pratique au théorique
peut être source de difficultés pour certains.
Elle
nécessite le passage à une conception plus théorique : au cycle 3, la fraction
est reliée au fractionnement effectif d’une grandeur ; en sixième 7/3 est
le nombre qui multiplié par 3 donne 7 – ce passage du pratique au théorique
peut être source de difficultés pour certains.
 Interviennent
également des nombres décimaux au numérateur ou au dénominateur… et l’idée de
partage devient plus difficile à évoquer pour les élèves…
Interviennent
également des nombres décimaux au numérateur ou au dénominateur… et l’idée de
partage devient plus difficile à évoquer pour les élèves…
Évolution de la notion de nombre au cours de la scolarité ![]()
Pour conclure, sur l’apprentissage des nombres au cours de la scolarité obligatoire, je ferai deux remarques ou, si on veut, deux suggestions :
 un
temps insuffisant est consacré à travailler la compréhension, le sens au profit
d’un travail sur le vocabulaire et sur les techniques ;
un
temps insuffisant est consacré à travailler la compréhension, le sens au profit
d’un travail sur le vocabulaire et sur les techniques ;
 un
peu comme au cours de l’histoire, l’idée que l’élève se fait de ce qu’est un
nombre doit évoluer :
un
peu comme au cours de l’histoire, l’idée que l’élève se fait de ce qu’est un
nombre doit évoluer :
 le
passage des entiers naturels aux décimaux suppose de renoncer à l’idée de nombres
qui se suivent et d’accepter que le processus d’intercalation soit sans fin…
le
passage des entiers naturels aux décimaux suppose de renoncer à l’idée de nombres
qui se suivent et d’accepter que le processus d’intercalation soit sans fin…
 le
passage aux fractions quotients suppose d’accepter qu’un nombre ne s’exprime
pas nécessairement par une suite de chiffres ;
le
passage aux fractions quotients suppose d’accepter qu’un nombre ne s’exprime
pas nécessairement par une suite de chiffres ;
 le
passage aux négatifs suppose de renoncer au fait qu’un nombre exprime une quantité
ou une la mesure d’une grandeur.
le
passage aux négatifs suppose de renoncer au fait qu’un nombre exprime une quantité
ou une la mesure d’une grandeur.
Une synthèse sur les nombres est prévue en fin de collège, avec une ouverture sur les irrationnels, mais c’est tout au long de la scolarité obligatoire que ces évolutions qui sont aussi des ruptures devraient être prises en compte.
Deux questions
Le fait que les moyens de calcul numérique se soient profondément modifiés dans les pratiques quotidiennes, dans les pratiques professionnelles ou dans les pratiques scientifiques ne peut qu’interroger la place et le rôle donnés à l’apprentissage des différents moyens de calculer. Deux questions :
 Quels
sont les besoins en calcul du futur acteur social et professionnel ?
Quels
sont les besoins en calcul du futur acteur social et professionnel ?
 Quels
sont les besoins en calcul pour l’apprentissage des mathématiques ?
Quels
sont les besoins en calcul pour l’apprentissage des mathématiques ?
Apprendre à calculer comporte différentes facettes :
 c’est
d’abord apprendre à rendre calculables des situations par un travail de modélisation
(cf. résolution de problèmes) ;
c’est
d’abord apprendre à rendre calculables des situations par un travail de modélisation
(cf. résolution de problèmes) ;
 c’est
évidemment aussi apprendre à traiter des calculs, de façon automatisée ou raisonnée,
pour aboutir à un résultat exact ou approché ;
c’est
évidemment aussi apprendre à traiter des calculs, de façon automatisée ou raisonnée,
pour aboutir à un résultat exact ou approché ;
 c’est
aussi apprendre à organiser, à « programmer » un calcul pour le rendre
exécutable par une machine (cf. initiation à l’usage du tableur au collège).
c’est
aussi apprendre à organiser, à « programmer » un calcul pour le rendre
exécutable par une machine (cf. initiation à l’usage du tableur au collège).
Le tableau suivant offre un cadre permettant de penser les différents moyens de traiter un calcul :
| Calcul automatique |
Calcul réfléchi ou raisonné |
||
| Résultat exact |
Résultat approché |
||
| Calcul essentiellement mental |
Résultats mémorisés Procédures automatisées |
Procédures construites ou reconstruites choix des arrondis |
|
| Calcul papier-crayon |
Techniques opératoires (calcul posé) |
Procédures construites ou reconstruites choix des arrondis |
|
| Calcul machine |
calculs usuels |
Ex : division euclidienne avec calculatrice ordinaire |
|
Les programmes actuels, depuis le cycle 2 de l’école primaire, prévoient l’apprentissage et l’utilisation de ces trois moyens de calcul. Mais on constate, à l’école primaire :
 une
confusion entre calcul et calcul posé, ce dernier occupant l’essentiel des activités ;
une
confusion entre calcul et calcul posé, ce dernier occupant l’essentiel des activités ;
 une
pratique insuffisante du calcul mental ;
une
pratique insuffisante du calcul mental ;
 une
résistance des enseignants, voir un refus, vis-à-vis de l’utilisation des calculatrices.
une
résistance des enseignants, voir un refus, vis-à-vis de l’utilisation des calculatrices.
Les priorités définies dans les programmes ![]()
Les programmes définissent clairement les priorités (qui sont en rupture avec des pratiques fréquemment en usage dans les classes), en les justifiant et ces justifications valent sans doute pour le collège. En résumant :
Le calcul mental est la priorité des priorités pour au moins six raisons :
 c’est
un calcul d’usage, utile dans la vie ordinaire ;
c’est
un calcul d’usage, utile dans la vie ordinaire ;
 aucun
calcul écrit ne peut être effectué sans une disponibilité suffisante de résultats
connus ou obtenus mentalement : les erreurs dans la multiplication posée
sont plus souvent dues à des erreurs « de table » qu’à des erreurs
« de décalage » (près de 15 % des élèves, à l’entrée en Sixième) ;
aucun
calcul écrit ne peut être effectué sans une disponibilité suffisante de résultats
connus ou obtenus mentalement : les erreurs dans la multiplication posée
sont plus souvent dues à des erreurs « de table » qu’à des erreurs
« de décalage » (près de 15 % des élèves, à l’entrée en Sixième) ;
 le
calcul mental est le moyen privilégié pour contrôler un résultat obtenu par
un autre moyen ;
le
calcul mental est le moyen privilégié pour contrôler un résultat obtenu par
un autre moyen ;
 le
calcul mental réfléchi ou raisonné qui nécessite l’élaboration de stratégies
de calcul personnelles met en jeu l’initiative, le raisonnement et des connaissances
implicites ou explicites sur la numération et les propriétés des opérations c’est
le lieu principal d’établissement de relations entre calcul et raisonnement
;
le
calcul mental réfléchi ou raisonné qui nécessite l’élaboration de stratégies
de calcul personnelles met en jeu l’initiative, le raisonnement et des connaissances
implicites ou explicites sur la numération et les propriétés des opérations c’est
le lieu principal d’établissement de relations entre calcul et raisonnement
;
 le
calcul mental joue un rôle important dans l’appropriation de nouvelles connaissances,
que l’on songe par exemple à la perception rapide de rapports entre les nombres
dans le cas de la proportionnalité, de la simplification de fractions ou de
la factorisation d’expressions algébriques simples : le calcul mental est
ainsi une aide à la conceptualisation ; et on peut penser qu’un déficit
de compétences dans ce domaine constitue un handicap majeur pour de nombreux
élèves à l’entrée au collège ;
le
calcul mental joue un rôle important dans l’appropriation de nouvelles connaissances,
que l’on songe par exemple à la perception rapide de rapports entre les nombres
dans le cas de la proportionnalité, de la simplification de fractions ou de
la factorisation d’expressions algébriques simples : le calcul mental est
ainsi une aide à la conceptualisation ; et on peut penser qu’un déficit
de compétences dans ce domaine constitue un handicap majeur pour de nombreux
élèves à l’entrée au collège ;
 se
ramener à un cas calculable mentalement est souvent un bon moyen d’avancer dans
la résolution d’un problème.
se
ramener à un cas calculable mentalement est souvent un bon moyen d’avancer dans
la résolution d’un problème.
Le travail sur les techniques opératoires ![]()
Le travail sur les techniques opératoires doit être recentré dans deux directions :
 on
vise une bonne maîtrise dans des cas dits « simples » évitant à l’individu
de devenir esclave de la machine ;
on
vise une bonne maîtrise dans des cas dits « simples » évitant à l’individu
de devenir esclave de la machine ;
 on
insiste sur le travail de compréhension (de justification) de ces techniques
qui permet d’enrichir les connaissances mathématiques des élèves sur la numération
et sur les propriétés des opérations.
on
insiste sur le travail de compréhension (de justification) de ces techniques
qui permet d’enrichir les connaissances mathématiques des élèves sur la numération
et sur les propriétés des opérations.
L'apprentissage du calcul assisté par une machine ![]()
L’apprentissage du calcul assisté par une machine comporte quatre aspects :
 l’utilisation
d’une machine doit être contrôlée (c’est-à-dire sollicitée à bon escient et
avec un contrôle des résultats obtenus) ;
l’utilisation
d’une machine doit être contrôlée (c’est-à-dire sollicitée à bon escient et
avec un contrôle des résultats obtenus) ;
 dans
la résolution de problèmes, l’usage de la calculatrice est une aide (par exemple
pour explorer un phénomène numérique ou pour les élèves qui ont des faiblesses
en calcul, en leur permettant d’avoir malgré tout accès à une activité mathématique),
mais son utilisation nécessite une organisation particulière des calculs dont
il faut également penser à conserver une trace ;
dans
la résolution de problèmes, l’usage de la calculatrice est une aide (par exemple
pour explorer un phénomène numérique ou pour les élèves qui ont des faiblesses
en calcul, en leur permettant d’avoir malgré tout accès à une activité mathématique),
mais son utilisation nécessite une organisation particulière des calculs dont
il faut également penser à conserver une trace ;
 certaines
de ses fonctionnalités nécessitent un apprentissage spécifique ou peuvent en
faire l’objet (facteurs constants, mémoire) ;
certaines
de ses fonctionnalités nécessitent un apprentissage spécifique ou peuvent en
faire l’objet (facteurs constants, mémoire) ;
 elle
peut être source de problèmes intéressants, par exemple comment calculer 247
x 39 avec la machine, sans utiliser la touche [ x ].
elle
peut être source de problèmes intéressants, par exemple comment calculer 247
x 39 avec la machine, sans utiliser la touche [ x ].
Le cadre proposé pour l’école primaire peut sans doute trouver des prolongements tout au long de la scolarité au collège. Certains IREM ont d’ailleurs entrepris des travaux sur une utilisation plus importante et organisée du calcul mental.
Apprentissage du calcul au primaire ![]()
Quelles opérations ont été travaillées à l’école primaire (sens et moyens de calcul) ?
Ce tableau résume la situation (nouveaux programmes) :
| Entiers naturels |
Décimaux |
|
| addition |
Depuis le cycle 2
|
Fin du cycle 3
|
| soustraction |
Depuis le cycle 2
Depuis le début du cycle 3
|
Fin du cycle 3
|
| multiplication |
Depuis le cycle 2
Depuis le début du cycle 3
|
Fin du cycle 3 : multiplication d’un décimal par un entier
Collège Produit de 2 décimaux (sens et calculs) |
| division |
Cycle 3 : division euclidienne
|
Collège Quotient décimal de 2 entiers et quotient de 2 décimaux (sens et calculs) |
L'extension du calcul aux décimaux suppose des restructurations
de compétences ![]()
L’extension du calcul à de nouveaux nombres (décimaux, puis fractions et relatifs) ne s’opère pas en simple prolongement des significations établies antérieurement. Elle suppose le plus souvent des remises en cause et donc des restructurations de connaissances établies.
Pour la multiplication ou la division par un décimal, la question du sens doit faire l’objet d’une attention particulière : par exemple, au cycle 3, l’idée de multiplication est attachée à celle d’addition itérée et au mot « fois »… Ce qui est difficilement extensible au cas du produit par un décimal : itérer 3,5 fois se conçoit encore ; 2,048 fois plus difficilement et 0,706 fois encore plus difficilement.
L’utilisation de cette nouvelle multiplication dans des situations doit donc être justifiée… Elle nécessite un recours à la proportionnalité, par exemple :
Pour calculer le prix de 0,706 kg de gruyère à 9,85 € le kg, il est possible de considérer qu’on achète 7/10 de kg et 8/1000 de kg (la signification des fractions comme un dixième de kg pris 7 fois justifie la multiplication) ou que si on calcule 9,85 x 706, on a le prix de 706 kg et qu’en divisant par 1 000, on a celui de 0,706 kg (ce qui rejoint la justification de la technique… et montre que travail sur le sens et travail sur la technique vont souvent de pair)…
De même, des théorèmes implicites qui ont fonctionné durant une partie importante de la scolarité comme « la multiplication agrandit » et « la division diminue » doivent être remis en cause.
L’enseignement doit être attentif à ces restructurations nécessaires et en faire des enjeux d’apprentissage.
Les compétences en calcul mental à l’entrée en Sixième ![]()
La maîtrise des tables et de ce qui doit être mémorisé n’est pas ou peu évaluée en tant que telle, mais on sait que celle des tables de multiplication n’est pas complète pour tous les élèves, notamment sous ses différents aspects :
 donner
un produit ;
donner
un produit ;
 donner
un facteur d’un produit ;
donner
un facteur d’un produit ;
 donner
les décompositions d’un nombre sous forme de produits.
donner
les décompositions d’un nombre sous forme de produits.
On peut relever qu’un résultat comme le quart de 100 n’est connu ou rapidement retrouvé que par 67 % des élèves (entrée en Sixième, 2000).
Concernant le calcul réfléchi (recherche de résultats exacts), les résultats sont contrastés.
En 2002
| 198 + 10 |
est réussi |
par 84 % des élèves |
| 405 – 10 |
par 81 % |
|
| 47 + 33 |
par 86 % |
|
| 60 – 19 |
seulement par 67 % |
En 2000,
| 52 : 4 |
n’était réussi que par 35 % |
Lorsque des nombres décimaux sont en jeu, comme résultats ou dans les calculs, les résultats sont moins bons.
En 2002
| 37 : 10 |
est réussi |
par 56 % des élèves (par seulement 42 % en 2003, année au cours de laquelle les résultats sont en baisse générale – mouvement du printemps 2003 ?) |
| 3 fois 0,5 |
par 46 % |
|
| 1,7 + 2,3 |
par 64 % |
|
| 2,5 x 4 |
par 49 % |
Le calcul approché fait l’objet d’une première approche à l’école primaire. Il est déstabilisant pour les élèves dans la mesure où, pour chaque calcul, des résultats différents sont considérés comme acceptables. Enfin ce calcul ne doit pas être développé pour lui-même, mais dans des situations qui correspondent à ses fonctions principales :
 fournir
une estimation, suffisante dans certaines situations dans lesquelles la réponse
exacte n’est pas nécessaire ;
fournir
une estimation, suffisante dans certaines situations dans lesquelles la réponse
exacte n’est pas nécessaire ;
 permettre
des anticipations ;
permettre
des anticipations ;
 être
utilisé comme moyen de contrôle d’un résultat obtenu « à la main »
ou avec une machine.
être
utilisé comme moyen de contrôle d’un résultat obtenu « à la main »
ou avec une machine.
Conclusion : l’entraînement au calcul mental sous ses 2 formes (mémorisé et réfléchi) et ses deux types de résultats (exacts et approchés) doit impérativement être poursuivi de façon régulière au collège. En particulier, se pose la question des résultats dont la mémorisation doit être entretenue et de ceux, nouveaux, dont la mémorisation est utile (carrés, racines carrées, puissances de nombres simples…)
Concernant le calcul posé
Il n’est pas évalué en 2002 et 2003.
En 2000 et 2001, les résultats montrent que l’addition et la soustraction sont calculées correctement par 80 % à 90 % pour les entiers et par 60 % à 80 % pour les décimaux.
La multiplication sur les entiers pose davantage problème : 64 x 39 n’est réussi que par 54 % des élèves (2001) et 523 x 305 par 61 % (2000) – les tables sont plus difficiles dans le 1er calcul que dans le 2e –
Pour la division, il faut remonter aux évaluations de 1999 qui montrent de grands écarts selon la difficulté des calculs :
73 : 3 est réussie par 76 % des élèves alors que 2782 : 3 ne l’est que par 44 %.
Conclusion
1) Le calcul posé, dans des cas raisonnables, doit donc continuer à être entraîné au collège, notamment pour la multiplication et la division.
2) Si on ne veut pas accroître les difficultés il faut doser ce que l’on demande de calculer « à la main » et ce que l’on permet de calculer « à la machine ».
Prise en compte du long terme et évolution des procédures de résolution
On peut difficilement envisager la question du calcul sans évoquer la résolution de problèmes. Le calcul peut être un objet d’étude, mais le plus souvent il intervient comme outil pour traiter des situations (rapport avec le réel, avec d’autres disciplines et, plus particulièrement, avec la mesure des grandeurs).
J’ai déjà évoqué la question de ce qu’on a coutume d’appeler le « sens des opérations », en soulignant que ce sens était à reconstruire lorsque de nouveaux nombres interviennent. Les travaux de Gérard Vergnaud ont montré que, même si on se limite à l’opération la plus élémentaire (l’addition), la maîtrise des problèmes dans lesquels cette opération intervient comme moyen de résolution s’opère sur une très longue période temps.
Exemple
(entrée en Sixième 1994) :
Lucie aime jouer aux billes. A la fin de la journée, elle a 8 billes de plus que le matin.
Pourtant la journée avait mal commencé : à midi, elle avait perdu 2 billes !
Que s’est-il passé l’après-midi ?
21 %
Proposé à des élèves de l’école primaire, la résolution de ce problème nécessite la mise en œuvre d’un raisonnement, par exemple : L’après-midi, elle a dû regagner les 2 perdues le matin, puis encore 8 autres, donc en gagner 10.
Proposé plus tard, il peut être modélisé et résolu à l’aide nombres relatifs …
(-2) + … = (+8), puis résolution par raisonnement ou par essai
et, plus tard encore, en utilisant une mise en équation : (-2) + x = (+8), puis résolution.
Je m’attacherai plutôt à un constat et une tentative d’analyse qui peuvent déboucher sur des perspectives pour l’enseignement.
Il nous est fourni, de façon constante, par toutes les évaluations (françaises ou internationales) : la résolution de problèmes est le principal lieu de difficulté pour nos élèves… alors que c’est l’enjeu principal de notre enseignement.
Deux exemples suffisent à caractériser les difficultés rencontrées.
Exemple 1
Les images (résultat 2003)
Xavier range les 50 photos de ses dernières vacances dans un classeur.
Chaque page contient 6 photos.
a) Combien y aura-t-il de pages complètes ?
b) Combien y a-t-il de photos sur la page incomplète ?
Il y a .......... pages complètes : 54 %
Il y a .......... photos sur la page incomplète : 57 %
Ce résultat est très faible compte tenu des connaissances que les élèves peuvent mobiliser pour le résoudre :
 schéma
et dénombrement ;
schéma
et dénombrement ;
 addition
itérée ;
addition
itérée ;
 essais
de produits ;
essais
de produits ;
 division.
division.
Il montre ce que confirme l’observation des productions : le fait que les élèves n’utilisent pas tout ce qu’ils savent pour affronter un problème. Résoudre un problème, c’est plus écrire un calcul… que chercher la solution, éventuellement par des moyens non experts. Au-delà des difficultés de lecture ou de la maîtrise du sens des opérations, c’est l’autonomie des élèves face à ce type d’activité qui paraît en cause.
Exemple 2
Raisonnement (résultat 2000)
Sophie a dessiné et colorié trois étiquettes rectangulaires
toutes identiques sur une plaque de carton, comme le montre le dessin. La plaque
est rectangulaire et a pour longueur
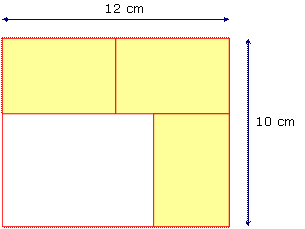
a) Calcule la longueur réelle d’une étiquette. Écris tes calculs. 44 %
b) Calcule la largeur réelle d’une étiquette. Écris tes calculs. 23 %
22 % des élèves ont mesuré.
Trois difficultés :
 la
notion de schéma,
la
notion de schéma,
 le
fait qu’une mesure puisse être obtenue par un calcul et non par un mesurage,
le
fait qu’une mesure puisse être obtenue par un calcul et non par un mesurage,
 la
capacité à opérer des déductions, donc à raisonner.
la
capacité à opérer des déductions, donc à raisonner.
Ce qui fournit deux pistes de travail pour le primaire et le début du collège :
 inciter
les élèves à initier des procédures de résolution originales, personnelles (cf.
programme du primaire) lorsque la solution experte n’est pas connue ou pas reconnue
par l’élève (le problème ne doit pas toujours être un problème d’application
des connaissances du chapitre !) ;
inciter
les élèves à initier des procédures de résolution originales, personnelles (cf.
programme du primaire) lorsque la solution experte n’est pas connue ou pas reconnue
par l’élève (le problème ne doit pas toujours être un problème d’application
des connaissances du chapitre !) ;
 travailler
la capacité à déduire et à résoudre certains problèmes en articulant différentes
étapes par un raisonnement approprié.
travailler
la capacité à déduire et à résoudre certains problèmes en articulant différentes
étapes par un raisonnement approprié.
Le cas de la proportionnalité à l’articulation de l’école et du
collège ![]()
À l'école primaire, la proportionnalité n’est pas étudiée pour elle-même.
Les élèves sont confrontés à des problèmes qu’ils résolvent en utilisant des raisonnements appuyés implicitement sur des propriétés de la proportionnalité :
 les
propriétés de linéarité sont celles qui sont le plus souvent utilisées :
idée de "fois plus" (si j'achète trois fois plus d'objets, je
paierai une somme trois fois plus importante...) ;
les
propriétés de linéarité sont celles qui sont le plus souvent utilisées :
idée de "fois plus" (si j'achète trois fois plus d'objets, je
paierai une somme trois fois plus importante...) ;
 le
passage par l’image de l’unité ;
le
passage par l’image de l’unité ;
 le
coefficient de proportionnalité est également utilisé, en particulier dans le
cas où est mise en jeu une relation entre grandeurs de même nature : mélanges
(cinq fois plus d'eau que de sirop), agrandissement ou réduction de figures
et échelles (les dimensions sur le papier sont cent fois plus petites que dans
la réalité).
le
coefficient de proportionnalité est également utilisé, en particulier dans le
cas où est mise en jeu une relation entre grandeurs de même nature : mélanges
(cinq fois plus d'eau que de sirop), agrandissement ou réduction de figures
et échelles (les dimensions sur le papier sont cent fois plus petites que dans
la réalité).
Des situations où ces types de raisonnement ne fonctionnent pas sont également proposées (situations de non proportionnalité).
La notion de proportionnalité, à la fin de l'école primaire, est donc liée au fonctionnement de certains types de raisonnements contextualisés, appuyés sur l’une des deux propriétés précédentes.
Dans cette optique, la reconnaissance d’une situation de proportionnalité n’est pas préalable à sa résolution : elle intervient au cours même de son traitement.
Exemple
Prendre 20 % de 350.
1
Pour 100 fabriqués à 20 vendus
Pour 100 fabriqués à 20 vendus
Pour 100 fabriqués à 20 vendus
Pour 300 fabriqués à 60 vendus
Pour 50 fabriqués à 10 vendus
Pour 350 fabriqués à 70 vendus
2
Pour 100 fabriqués à 20 vendus
Pour 300 fabriqués à 60 vendus (3 fois plus)
Pour 50 fabriqués à 10 vendus (la moitié)
Pour 350 fabriqués à 70 vendus
3
Le nombre de pains vendus, c'est 1/5 du nombre de pains fabriqués (ou 5 fois moins)
1/5 de 350, c'est 70
Au collège, les procédures de résolution évoluent au fur et à mesure que progressent les connaissances numériques des élèves. On se limite ici à mettre en évidence l’évolution des procédures de résolution.
Sixième
Traiter les problèmes « de proportionnalité », en utilisant des raisonnements appropriés, en particulier :
 passage
par l’image de l’unité
passage
par l’image de l’unité
 utilisation
d’un rapport de linéarité, exprimé sous forme de quotient
utilisation
d’un rapport de linéarité, exprimé sous forme de quotient
 utilisation
du coefficient de proportionnalité, exprimé sous forme de quotient
utilisation
du coefficient de proportionnalité, exprimé sous forme de quotient
Appliquer un taux de pourcentage : méthode « experte »
Les différentes propriétés n’ont pas à être formalisées.
Les rapports utilisés sont, soit des rapports entiers ou décimaux simples (2,5 par exemple qui peut être exprimé par « 2 fois et demie »), soit des rapports exprimés sous forme de quotient : le prix de 7 m de tissu est 7/3 fois le prix de 3 m de tissu
Cinquième
Procédures
 Utilisation
plus systématique des quotients
Utilisation
plus systématique des quotients
 Utilisation
de tableaux de nombres
Utilisation
de tableaux de nombres
 Première
approche graphique
Première
approche graphique
 calcul
d’un pourcentage (méthode « experte »)
calcul
d’un pourcentage (méthode « experte »)
Quatrième
 caractérisation
graphique
caractérisation
graphique
 produit
en croix (en lien avec égalité de quotients)
produit
en croix (en lien avec égalité de quotients)
Troisième
 modélisation
par une fonction linéaire
modélisation
par une fonction linéaire
Il faut y ajouter différents domaines où la proportionnalité permet de rendre compte du phénomène étudié : Thalès, trigonométrie, agrandissement et réduction de figures…
[i] On peut le montrer : partages et reports effectifs ; le « vivre », notamment dans le cas des fractions inférieures à 1 : deux façons de répartir équitablement 3 tartes rectangulaires entre 7 personnes ; on peut aussi le prouver, plus difficilement : 1/3 pris 3 fois c’est 1, donc 7 fois 1/3 reporté 3 fois c’est 7 (qui est la nouvelle définition de 7/3)
On trouvera à la page http://www.eduscol.education.fr/index.php?./D0048/primacc.htm du site Eduscol quelques documents de référence pour un travail sur l’articulation école-collège. Ils font partie du dossier "Les nouveaux programmes à l'école primaire"
 Articulation
école-collège (PDF, 163 Ko)
Articulation
école-collège (PDF, 163 Ko)
 Calcul
mental (PDF, 262 Ko)
Calcul
mental (PDF, 262 Ko)
 Utiliser
les calculatrices en classe (cycles 2 et 3) (PDF,
254 Ko)
Utiliser
les calculatrices en classe (cycles 2 et 3) (PDF,
254 Ko)
 Le
calcul posé (PDF, 303 Ko)
Le
calcul posé (PDF, 303 Ko)
 Les
problèmes pour chercher (PDF, 302 Ko)
Les
problèmes pour chercher (PDF, 302 Ko)
 Vers
les mathématiques-maternelle (PDF, 292 Ko)
Vers
les mathématiques-maternelle (PDF, 292 Ko)