Quelle est la somme des angles
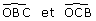 ?
?Que peux-tu déduire pour le triangle ABC ?
Soit I le milieu de [BC]. Construis le symétrique O' de O par rapport à I.
Quelle est la nature du quadrilatère BOCO' ?
Agencement d'un raisonnement déductif |
|
Clg Victor Louis, 33400 Talence |
|
Niveau
Cette activité a été créée en 1993 en classe de cinquième, dans le cadre d'un PAE portant sur le travail de l'écrit dans lequel quatre matières étaient impliquées, pour des élèves en difficulté faisant la classe en deux ans. Elle est aisément transposable à d'autres niveaux.
Objectifs
Pour l’élève :
# Mettre en évidence la différence entre démontrer et vérifier un résultat
# Être capable d'ordonner l'agencement d'un raisonnement déductif
Pour le professeur :
# Découvrir si le passage par l'écran apporte une aide aux élèves par rapport
à un travail sur papier.
Prérequis
Les notions mathématiques abordées dans l'exercice ont déjà été
rencontrées en classe.
Les élèves ont déjà travaillé sur traitement de texte. Notion de couper/coller
nécessaire.
Organisation pratique
Sept postes en réseau, deux élèves par poste + traitement de texte.
Description
Deux séances d’une heure. Il s'agit d'ordonner dix phrases écrites dans le désordre.
1ère heure : sept élèves devant l'écran et huit avec papier à découper.
# Sur l'écran les élèves déplacent les phrases pour établir une démonstration logique. La page écran est distribuée sur papier pour ne pas perdre des phrases avec une mauvaise manipulation.
# Au centre de la salle les huit autres élèves ont la même page écran. Ils découpent les phrases imprimées et les collent dans l'ordre correct.
2ème heure : Avec un deuxième texte d'exercice on intervertit les groupes.
Bilan
# Le travail fait par découpage est plus rapide
# 9 élèves sur 14 préfèrent le travail par découpage : c'est plus facile (manipulations), plus rapide (déplacement des phrases), plus clair (erreur de manipulation pour effacer les phrases déplacées à l'écran...).
# 5 élèves sur 14 préfèrent le travail sur ordinateur : plus concentré sur l'écran, plus propre comme résultat.
# 2 élèves sur 14 sont très gênés par les phrases imposées : "Si ça ne sort pas de ma tête, ça va pas...", "j'ai besoin de changer les phrases... les réponses déjà données m'ennuient et m'empêchent de raisonner...".
# 7 élèves sur 14 sont lassés par ce type d'exercice : "avec les 4 profs, c'est toujours du français, y en a marre !"..."
# Une grosse majorité reconnaît avoir progressé en expression écrite.
Construis un triangle isocèle BOC dont le sommet principal mesure
60°.
Quelle est la somme des angles 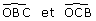 ?
?
Que peux-tu déduire pour le triangle ABC ?
Soit I le milieu de [BC]. Construis le symétrique O' de O par rapport à I.
Quelle est la nature du quadrilatère BOCO' ?
1. Souligne en rouge les hypothèses.
Combien dois-tu avoir de conclusions ?
2. Fais la figure.
3. Mets dans le bon ordre les phrases suivantes:
1. La somme des angles d'un triangle est 180°.
2. Alors 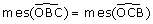 .
.
3. Dans un triangle isocèle les angles à la base ont la même mesure.
4. Les trois angles du triangle ABC mesurent 60°.
5. Alors 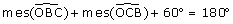
6. 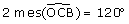
7. Donc 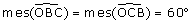
8. Donc ABC est équilatéral.
9. OBC est équilatéral et I est milieu du segment [BC], donc la médiane [OI] est aussi une hauteur.
10. Par construction, I est milieu des segments [BC] et [OO'].
11. Donc (OO') est perpendiculaire au segment [BC].
12. BOCO' a ses diagonales qui se coupent en leur milieu et qui sont perpendiculaires. Donc c'est un losange.
Soit ABCD un parallélogramme de centre O, I le milieu de [AB] et J
celui de [CD].
1) Construire ABCD avec AB = 8 cm, AD = 6 cm et 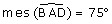 .
.
2) Par la symétrie de centre O, quel est le symétrique de [AB] ? du point I
?
En déduire que O est le milieu de [IJ].
3) Démontrer que AICJ est un parallélogramme.
1) Souligne en rouge les hypothèses.
Combien dois-tu avoir de conclusions ? Souligne-les au crayon.
2) Fais la construction.
3) Mets dans l'ordre les phrases suivantes :
1. Par hypothèse, I est milieu de [AB] et J milieu de [CD].
2. Par construction, dans la symétrie de centre O, [DC] est le symétrique de [AB].
3. Alors J est le symétrique de I par rapport à O.
4. La symétrie centrale conserve les milieux.
5. Donc O est le milieu de [IJ].
6. Alors [AB] est parallèle à [DC] et AB = DC.
7. Un parallélogramme a ses côtés opposés parallèles et de même longueur.
8. Donc AICJ est un parallélogramme.
9. Comme I est milieu de [AB] et J est milieu de [CD], AI est égal à JC et [AI] est parallèle à [JC].