Les différents types de raisonnement au collège
Tout au long du collège, la démonstration occupe une place importante
puisque, dès la classe de sixième, la mise en place de courtes séances déductives
permet d'initier les élèves au raisonnement. En géométrie, les chapitres « droites
parallèles et perpendiculaires, cercle, symétrie axiale » permettent à
l'élève de passer de la géométrie d'observation, enseignée à l'école, à une
géométrie de déduction. Des travaux « géométrico-déductifs » peuvent
aussi constituer un terrain privilégié pour aborder le raisonnement à l'aide
d'îlots déductifs bien circonscrits, notamment à propos de la comparaison de
longueurs et d'aires.
Au cycle central, on continue ce travail. Les activités géométriques
habituent l'élève à expérimenter, à conjecturer puis à démontrer. Il faut cependant
veiller à ce que l'élève ne confonde pas conjecture et théorème. Le recours
à plusieurs pas de démonstration amène à comprendre le changement de statut
d'une assertion au fil d'une démonstration : un résultat intermédiaire
est une conclusion dans un pas et une donnée dans un pas ultérieur. L'examen
de la compatibilité entre l'ordre et la multiplication oblige l'élève à procéder
par disjonction de cas. Des propriétés dont la réciproque est fausse, comme
dans le cas des quadrilatères particuliers, fournissent des occasions d'utiliser
le contre-exemple.
En classe de troisième, l'apprentissage des théorèmes et des différents
types de raisonnement se poursuit. Des résultats d'arithmétique comme l'irrationalité
de racine carrée de deux ou le théorème sur les fractions irréductibles, sont
autant d'occasions de familiariser les élèves avec le raisonnement par l'absurde.
A travers de nombreux exercices et ce, dès la sixième, l'élève a donc
l'occasion d'élaborer différents types de raisonnement : raisonnement déductif,
raisonnement par disjonction de cas, infirmation par mise en évidence d'un contre-exemple,
approche du raisonnement par l'absurde.
Ce n'est qu'au lycée, en classe de seconde, qu'il utilisera l'équivalence
logique. Il faudra attendre l'année de terminale pour mettre en place le raisonnement
par récurrence.
Les différents types de raisonnement à travers le cours
(démonstrations de propriétés et exercices d'application)
| |
Sixième |
Cinquième |
Quatrième |
Troisième |
Raisonnement déductif |
Utilisation des propriétés des droites parallèles et
perpendiculaires.
Utilisation des propriétés des symétries axiales.
Définition du cercle. |
Propriétés caractéristiques du parallélogramme et des
quadrilatères particuliers.
Caractérisation angulaire du parallélisme.
Somme des angles d'un triangle.
Concours des trois médiatrices d'un triangle.
Différence de deux nombres, opposé d'une somme, d'une
différence.
Somme et produit des nombres en écriture fractionnaire. |
Triangle et droite des milieux.
Triangle et parallèles.
Droites remarquables du triangle.
Triangle rectangle et cercle.
Le théorème de Pythagore et sa réciproque.
Distance d'un point à une droite.
Tangente à un cercle.
Effet de l'addition sur l'ordre.
Double distributivité. |
Composée de deux translations, composée de deux symétries
centrales.
Représentation graphique d'une fonction linéaire.
Réciproque du théorème de Thalès.
Propriétés des racines carrées.
Propriétés des diviseurs d'un nombre entier.
Relations trigonométriques.
Identités remarquables. |
Raisonnement par disjonction de cas |
Comparaison des décimaux |
Comparaison des nombres relatifs en écriture décimale.
Distance de deux points sur un axe et soustraction des
nombres relatifs.
Somme et produit des relatifs. |
Effet de la multiplication sur l'ordre. |
Théorème de Thalès.
Angle inscrit, angle au centre.
L'équation 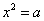 . .
Intersection de la sphère et du plan |
Mise en évidence d'un contre-exemple |
Exercices sur la division euclidienne |
Travail sur les propriétés caractéristiques des figures.
Prouver que deux suites de nombres ne sont pas proportionnelles. |
Travail sur des égalités fausses avec les puissances |
Travail sur des égalités fausses avec les racines carrées.
Les réciproques fausses des propriétés des diviseurs
d'un nombre entier. |
Approche du raisonnement par l'absurde |
|
Construction de triangles impossible.
Caractérisation angulaire du non parallélisme. |
Théorème de Pythagore. |
Théorème de Thalès.
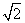 est irrationnel. est irrationnel.
Si on divise le numérateur et le dénominateur d'une fraction
par leur PGCD, on obtient une fraction irréductible égale. |
![]() .
.![]() est irrationnel.
est irrationnel.