Traitement de texte et mathématiques |
|
Collège de Saint Loubès (33) |
|
Niveau
Expérimenté avec une classe de cinquième sur nanoréseau en 1993 puis actualisé aux nouveaux environnements, ce type d’activité reste d'actualité mais s’adresse plutôt à des élèves de quatrième et même au-delà.
Objectifs
À partir d'une figure simple, composer une démonstration de géométrie en utilisant un traitement de texte.
Prérequis
Avoir déjà utilisé le traitement de texte, en connaître les fonctionnanlités de base, en particulier être familier avec la notion de copier/coller ou d’importation de documents.
Organisation pratique
Quinze ordinateurs en réseau ; traitement de texte connu des élèves ; salle équipée d’un système de rétroprojection.
Description
Cette activité vise à apprendre aux élèves à faire le bon choix d'un théorème parmi une liste et à n'utiliser que ceux qui sont nécessaires.
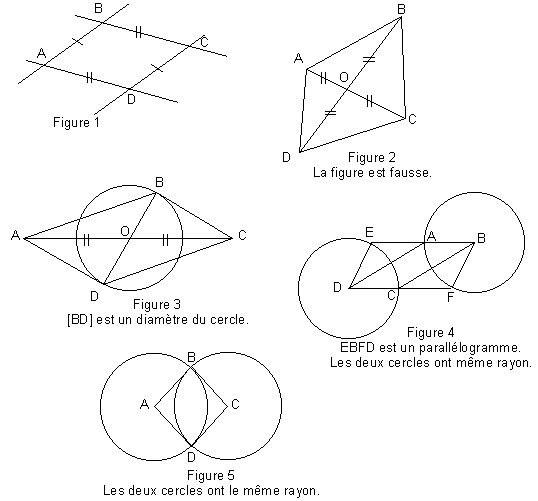
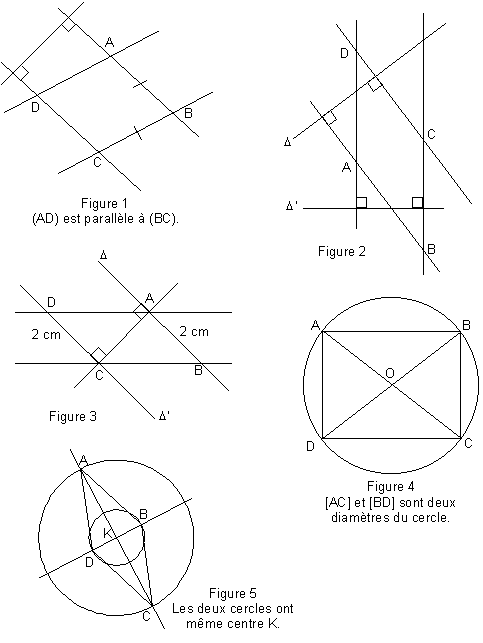
L'élève dispose, sur papier, d’une liste de théorèmes et d'une fiche contenant les figures de cinq démonstrations à trouver.
À l’aide du traitement de texte, il doit compléter un fichier (dans l’expérimentation le fichier était préparé, au nom de l’élève ; on peut aussi le faire créer). Pour chaque exercice, l’élève doit écrire les données, la conclusion et élaborer la démonstration en choisissant, dans la liste fournie, le ou les théorèmes appropriés. Il n'a pas besoin de taper les théorèmes : il les récupère dans la base fournie.
La base de théorèmes peut être fournie de deux façons :
# Chaque théorème est contenu dans un fichier protégé en écriture (Th01, Th01, Th02, …). L’élève récupère ces théorèmes grâce à la commande « importer » du traitement de texte (c’est l’option qui a été retenue dans l’expérimentation, le copier/coller présentant des difficultés pour certains élèves).
# Les théorèmes sont contenus dans un document accessible en réseau, protégé en écriture, et l’élève travaille sur deux fichiers en même temps par copier/coller (nécessite plus de dextérité de la part des élèves).
Pour chaque théorème employé, il doit ajouter la conclusion propre à l'exercice. Le traitement de texte permet de revenir en arrière pour ajouter (ou enlever) des théorèmes.
Le travail de chacun est imprimé à la fin et la correction se fait au tableau ou à l’aide du système de vidéoprojection.
Bilan et remarques
Ce type d'activité peut évidemment se faire uniquement sur papier, mais le travail sur traitement de texte apporte une dimension ludique. On a pu constater que les élèves sont plus attentifs à ce qu'ils composent et qu’ils ont l'impression de ne pas être en échec face à une démonstration de géométrie. De plus, ils rendent un travail propre et concis.
Pour que l'élève prenne conscience qu'il s'agit bien d'un travail, il convient de réintégrer ces figures dans les contrôles. Certains reprennent alors d'instinct la même démonstration ; d'autres, hélas !, ne voient pas la similitude.
Cette activité est adaptable à d'autres listes de théorèmes et d'autres exercices.
Il est à noter que les jeunes élèves ont des difficultés à se déplacer à l'écran, à gérer plusieurs fenêtres, pour aller chercher un bloc qu'il n'ont pas devant les yeux. Même si les élèves ont pour la plupart travaillé sur traitement de texte en technologie, il faut faire des rappels et en particulier réexpliquer certaines notions de base.
Il s'est avéré nécessaire de faire faire aux élèves, en liaison avec les professeurs de lettres un travail sur les conjonctions de coordination. Nous avons essayé qu'il n'y ait pas d'ambiguïté mais cela n'a pas été toujours évident. Les fiches correspondantes figurent en fin de document.
Après avoir lancé le traitement de texte, ouvre le fichier à ton nom.
1) Pour chacun des exercices suivants, tape au clavier les données et la conclusion qui sera du type : "ABCD est un ............"
2) Dans la liste qui est près de toi, choisis la ou les propriétés
qui te permettent de passer des données à la conclusion.
Insère cette propriété en te servant de la commande "importer" du
traitement de texte. Le nom que porte le fichier est écrit à côté de la propriété.
Quand tu as exploité une propriété, tu complètes par "donc ..................."
Après chaque manipulation d'importation sauve ton travail.
3) Ta dernière phrase doit être : "Donc ABCD est un ......."

Après avoir lancé le traitement de texte, ouvre le fichier à ton nom.
1) Pour chacun des exercices suivants, tape au clavier les données et la conclusion qui sera du type : "ABCD est un ............"
2) Dans la liste qui est près de toi, choisis la ou les propriétés
qui te permettent de passer des données à la conclusion.
Insère cette propriété en te servant de la commande "importer" du
traitement de texte. Le nom que porte le fichier est écrit à côté de la propriété.
Quand tu as exploité une propriété, tu complètes par "donc ..................."
Après chaque manipulation d'importation sauve ton travail.
3) Ta dernière phrase doit être : "Donc ABCD est un ......."
| Th01 |
Si un quadrilatère a ses diagonales qui se coupent en leur milieu alors c'est un parallélogramme. |
| Th02 |
Si un quadrilatère a ses côtés opposés parallèles alors c'est un parallélogramme. |
| Th03 |
Si un quadrilatère non croisé a deux côtés parallèles et égaux alors c'est un parallélogramme. |
| Th04 |
Si un quadrilatère non croisé a ses côtés opposés de même longueur alors c'est un parallélogramme. |
| Th05 |
Si un quadrilatère non croisé a ses angles opposés de même mesure alors c'est un parallélogramme. |
| Th06 |
Si un quadrilatère a trois angles droits alors c'est un rectangle. |
| Th07 |
Si un parallélogramme a un angle droit alors c'est un rectangle. |
| Th08 |
Si un parallélogramme a ses diagonales de même mesure alors c'est un rectangle. |
| Th09 |
Si un quadrilatère a ses quatre côtés de même mesure alors c'est un losange. |
| Th10 |
Si un parallélogramme a ses diagonales perpendiculaires alors c'est un losange. |
| Th11 |
Si un parallélogramme a deux côtés consécutifs de même longueur alors c'est un losange. |
| Th12 |
Deux droites perpendiculaires à une même troisième sont parallèles. |
| Th13 |
Le centre d'un cercle est milieu de tout diamètre du cercle. |
| Th14 |
Les côtés opposés d'un parallélogramme sont parallèles. |
| Nom : |
Classe : |
Les conjonctions de coordination sont : MAIS, OU, ET, DONC, OR, NI, CAR.
Relier chaque couple de propositions par une conjonction de coordination :
1. La salle n'est pas ouverte au public on y fait des travaux.
2. Je ferai deux choses pour vous : je participerai à votre réunion je signerai votre pétition.
3. Laure a un bouton sur la joue elle est si bien maquillée que cela ne se voit pas.
4. Ayant peu de temps, je ne pourrai tout visiter : je verrai le musée j'irai au zoo.
5. Le médecin dit que tu es guéri et ton père déclare que tu peux sortir ; tu peux venir avec nous.
6. Nous n'avons pas cours d'histoire aujourd'hui le professeur est absent.
7. Certains élèves de cette classe ne sont pas châtains, blonds.
8. Cet épicier n'avait plus guère de clients, il a fermé son magasin.
9. Cette figure de géométrie est un triangle elle a trois côtés et trois angles.
10. Cet élève est timide il a pris la parole pour défendre son ami.
11. Joue au tennis va à la pêche fais du sport.
12. Delphine se dépêche elle craint de manquer le ramassage.
| Nom : |
Classe : |
Dans le texte suivant remplace les cases par les mots CAR ou DONC et aussi par les réponses aux problèmes.
1. Jean a 24 ans de moins que son père. Jean a 14 ans. son père a ans.
2. ABCD est un parallélogramme les deux côtés [AB] et [CD] sont
3. Ce nombre est divisible par 3 la somme de ses chiffres est 12.
4. Ce nombre se termine par 5 il est divisible par
5. Les trois longueurs AB, CB et AC sont égales ce triangle est
6. 0 n'a pas d'inverse une division par 0 n'a aucun sens.
7. Un tiers est plus que un quart trois est plus que quatre.
8. Un nombre positif est plus qu'un nombre négatif +8 est plus que -5.
9. Paul est l'aîné d'une famille de trois enfants. Jean est le plus jeune. Leur frère Laurent a trois ans. Jean a moins de trois ans il est le benjamin. Laurent a deux ans de moins que Paul. Il a ans.
10. (AB) est parallèle à (CD) mais (AD) et (BC) sont sécantes donc ABCD est un [AC] et [BD] n'ont pas le même milieu ABCD n'est pas un
11. (AB) et (CA) sont perpendiculaires ABC est un triangle L'hypoténuse de ce triangle est [BC] c'est le côté à l'angle droit.
12. L'angle A mesure 20 degrés et l'angle B mesure 70 degrés les deux angles sont
13. Cette fraction est irréductible je ne peux plus la simplifier.
14. Deux angles A et B sont supplémentaires. A mesure 120 degrés B mesure . L'angle B est saillant il mesure moins de 90 degrés.
15. L'angle A mesure 120 degrés. Il est saillant il mesure moins de 180 degrés.