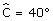 .
.2. Marquer le point R tel que C soit le milieu du segment [BR].
3. A l'extérieur du triangle ABC, placer le point S tel que BS = SA et
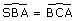 .
.4. Que peut-on dire des droites (SB) et (BR).
Traitement de texte et mathématiques (2) |
|
Clg Victor Louis, 33400 Talence |
|
Niveau
Cinquième, mais cette activité est réalisable à d'autres niveaux.
Objectifs
Apprendre aux élèves à rédiger une démonstration : utiliser un vocabulaire précis, construire des phrases d'explication.
Prérequis
Notions élémentaires de cinquième sur le triangle rectangle,
les droites perpendiculaires, les droites parallèles, les quadrilatères particuliers,...
Travail antérieur sur le traitement de texte. Notion de couper/coller nécessaire.
Organisation pratique
Salle équipée de 15 ordinateurs en réseau.
Durée : 4 h
Description
Les exercices proposés aux élèves pendant l'année scolaire ne figurent pas tous ici. Ils sont de plusieurs types :
# Pour apprendre un vocabulaire précis : textes à trous à compléter, textes incomplets, sans trous apparents, avec ponctuation, à compléter.
# Pour construire des phrases d'explication : phrases complètes, dans l'ordre, sans ponctuation, à ponctuer.
# Pour apprendre à mettre en ordre un raisonnement : phrases complètes, avec ponctuation, dans le désordre d’une part et, d’autre part, phrases complètes, sans ponctuation, dans le désordre.
Trois activités, étalées sur quatre séances, accompagnées de leur description, sont proposées dans les pages qui suivent. Elles comportent une partie recherche en compagnie du professeur ou à la maison et une partie travail sur ordinateur.
Bilan et remarques
Les travaux proposés pourraient être faits exclusivement sur
papier, mais les élèves sont plus concentrés devant l'écran et font moins d'erreurs.
L'exercice à trous a été profitable pour l'utilisation d'un vocabulaire précis.
L'utilisation de l'outil informatique est apprécié par tous les élèves et la
demande est grande. Il permet de varier la présentation des leçons, les méthodes
d'apprentissage, les méthodes de mémorisation.
Le type d'exercices proposés s'est avéré très formateur en géométrie.
Reconstruire le texte avec un retour à la ligne pour chaque action demandée.
1. Revenir à la ligne après chaque action.
2. Construire une phrase par action, en ajoutant verbe, majuscule, ponctuation. Effacer les mots devenus inutiles.
3. Imprimer deux exemplaires du texte fini. Sur un exemplaire, souligner dans chaque phrase le ou les mots clefs.
Trace un triangle ABC rectangle en A, puis une perpendiculaire à (AB) passant par B, et une parallèle à (AB) passant par C. Soit P l'intersection des deux droites tracées. Quelle est la nature du quadrilatère ABPC ?
Après avoir cherché la démonstration à la maison, compléter le "texte
à trous" de la démonstration (cette fois-ci les mots à utiliser ne sont
pas donnés).
Précaution : Avoir le texte correct en entier sur la disquette. À imprimer pour
une autocorrection.
Comme ABC est rectangle en A, (AB) est perpendiculaire à (AC). Par
hypothèse (BP) est perpendiculaire à (AB).
Si deux droites sont perpendiculaires à une même troisième alors elles sont
parallèles entre elles. Donc (AC) est parallèle à (BP). Par construction (CP)
est parallèle à (AB).
Le quadrilatère ABPC a ses côtés parallèles deux à deux. C'est donc un parallélogramme.
Comme il a deux angles droits, c'est un rectangle.
................ABC ................................... A, (AB) est perpendiculaire à (AC). ......................... (BP) est perpendiculaire à (AB).
Si deux droites sont ................................ à une même troisième alors elles sont ........................... entre elles. Donc (AC) est parallèle à (BP). ................................ (CP) est parallèle à (AB).
Le ................ ABPC a ses côtés ...................... deux à deux. C'est ......... un ................................. Comme il a deux ............................... c'est un .................................
1. Tracer un triangle ABC, rectangle en A, tel que AC = 6 cm
et 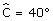 .
.
2. Marquer le point R tel que C soit le milieu du segment [BR].
3. A l'extérieur du triangle ABC, placer le point S tel que BS = SA
et 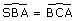 .
.
4. Que peut-on dire des droites (SB) et (BR).
1. Recherche à main levée. Construction de la figure.
2. Écrire au tableau les données. Conclusion.
(15 mn)
3. Passage aux ordinateurs.
1. Retour à la ligne pour chaque phrase.
2. Sauter une ligne entre chaque phrase.
3. Ordonner les phrases.
4. Imprimer le texte fini.
[BS) et [BR) sont perpendiculaires. Soit ABC + ACB = 90. Le triangle ABC est rectangle en A, la somme de ses angles aigus est 90°. Comme ACB = 40° alors ABC = 90 - 40. ABC = 50°. SBR = 90 = 40 + 50 = SBA + ABC. Je sais que SBA = BCA = 40°;
1. Construire un triangle ABC tel que AB = 7 cm,
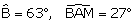 , M étant le milieu
de [BC].
, M étant le milieu
de [BC].
2. Quelle est la nature du triangle ABC ?
1. Construction au centre de la classe. J'observe que 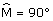 et que BAC est isocèle
A.
et que BAC est isocèle
A.
2. Je le démontre. Passage aux ordinateurs.
La démonstration est écrite dans le désordre, sans ponctuation.
1. Placer les points, les virgules.
2. Retour à la ligne pour chaque phrase, chaque égalité.
3. Sauter une ligne entre chaque phrase.
4. Ordonner les phrases, les égalités.
5. Imprimer le texte fini.
Le triangle ABC est isocèle en A je sais que M est le milieu de [CB] alors [AM] est une médiane dans un triangle la somme des angles est égale à 180° alors AMB = 180 - (27 + 63) AMB = 180 - 90 dans le triangle ABM je sais que MAB = 27° ABM = 63° donc [AM] est la hauteur issue de A le triangle ABC a la hauteur [AM] qui est aussi la médiane