Document professeur

Pour des raisons techniques, les chapeaux ne sont pas marqués sur les angles dans le document professeur.

1. Mise en évidence de la propriété « deux angles inscrits dans un cercle, interceptant un même arc, sont égaux »

Construire un cercle de centre O. Trois points sur le cercle (point sur objet).

Définir l'angle inscrit BAC (tracer les segments, marquer l'angle BAC, le mesurer).
Faire varier A sur le cercle puis dans le disque et hors du disque après avoir supprimé sa liaison avec le cercle (Choisir point dans la rubrique Redéfinir un objet du menu construction). Faire réagir les élèves. Que se passe-t-il lorsque l'on éloigne A ?

Premières conjectures : où sont situés les points A pour que l'angle BAC ait une mesure constante ?

Faire varier B ou C sur le cercle puis à nouveau A sur le cercle.
De quoi la mesure de l'angle BAC dépend-elle ?

Prendre deux autres points E et F sur l'arc BC qui contient A. Montrer les égalités d'angles obtenues..

Pour simplifier les manipulations, on peut créer une macro qui, à partir de 3 points, trace les côtés de l’angle, marque cet angle et affiche sa mesure (voir la macro Tracer_et_mesurer_un_angle.mac).

Par conjectures successives, les élèves sont capables d'énoncer la propriété « deux angles inscrits dans un cercle, interceptant un même arc, sont égaux ».

2. Mise en évidence de la propriété « l'angle inscrit dans un cercle est égal à la moitié de l'angle au centre correspondant ».

Effacer la figure précédente.
Tracer un cercle de centre O et trois points A, B, C, de ce cercle.
Comparer les angles BAC et BOC après les avoir marqués et mesurés.
Faire varier A, puis B, puis C sur le cercle.
Les élèves émettent les conjectures correspondantes.

Lorsqu'on fait varier A sur le cercle, sur le grand arc ou le petit arc BC, insister sur l'arc intercepté et sur l'angle au centre correspondant (saillant ou rentrant).

Pour faire apparaître les mesures des deux angles, saillants et rentrants, tracer deux marques en désignant les trois mêmes points mais dans un ordre inverse, puis déplacer une des deux marques vers l’angle rentrant (cf. anglins2.fig).

3. Démonstration des trois propriétés

Voir fiche élèves.

Document élève

A. Angle inscrit

Construisez un cercle, C, de centre O et trois points distincts A, B, C, de ce cercle.

B. Angle au centre et angle inscrit

Le professeur a fait varier A, puis B, puis C sur le cercle.
Quelles remarques avez-vous faites ?
Mesurez ces angles sur votre dessin.

C. Démonstration

Dessiner et mesurer n'est pas démontrer, d'autant que les mesures effectuées ne sont pas très précises. Vous allez maintenant démontrer les propriétés conjecturées.

Refaites une figure. La droite (OA) coupe le cercle C en D.
Quelle est la nature des triangles AOB et AOC ?

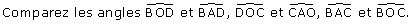
Ce dernier résultat permet d'énoncer la propriété (1) : ....

Démontrez alors l'autre propriété (propriété (2) : ...).