Exercice 1

(Recherche individuelle, mise en commun des résultats)

Tracer un triangle quelconque ABC.
Où se trouvent les centres des cercles passant par les points A et B ?
Où se trouvent les centres des cercles passant par B et C ?
Faire tracer les médiatrices des segments [AB] et [BC] , appeler O le point d'intersection. Montrer que OA = OB et que OB = OC. En déduire que le point O appartient aussi à la médiatrice du segment [AC]

En déduire que :
Dans tout triangle, les trois médiatrices sont concourantes en un point O qui est centre du cercle circonscrit au triangle.

Exercice 2

(Collectif)

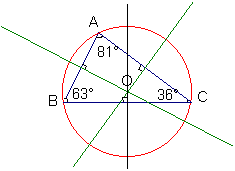
A l'aide du logiciel Le géomètre (à partir de la figure CerclCi1.fig), déterminer des positions particulières du point O centre du cercle circonscrit au triangle ABC.
Deux positions particulières se dégagent :
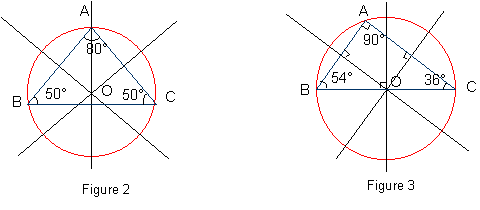
O est sur une des médiatrices, on obtient alors un triangle isocèle.(Cf  Cerclci2.fig), Figure 2
O est sur un des côtés, on obtient alors un triangle rectangle.(Cf Cerclci3.fig), Figure 3.

Exercice 3

Soit ABC un triangle rectangle en A, et soit O le milieu de l'hypoténuse. Tracer le point D symétrique de A par rapport à O.
Que peut-on dire des diagonales [AD] et[BC], du quadrilatère ABDC. En déduire que les longueurs OA, OB OC sont égales.

En déduire que :
Dans un triangle rectangle, le centre du cercle circonscrit est le milieu de son hypoténuse.

Exercice 4

Tracer un triangle rectangle ABC et les médiatrices des côtés [AB] et [AC].
Appeler O le point d'intersection de ces deux médiatrices. Que représente le point O pour le triangle ABC.

En déduire que :
Dans un triangle rectangle, les médiatrices des côtés de l'angle droit se coupent au milieu de l'hypoténuse.

Exercice 5

Un peintre se trouve au milieu de l'échelle de 4 mètres de long lorsque celle-ci se met à glisser le long du mur.
Quelle est la trajectoire suivie par ce peintre lors de la chute de son échelle ?
La principale difficulté de cet exercice est davantage dans la découverte de cette trajectoire que dans le démonstration en elle même.
La figure CerclCi4.fig permet de dessiner le lieu du milieu de l'échelle quand sa base glisse sur le sol, et donc de surmonter cette difficulté.

Exercice 6

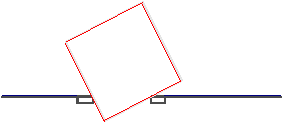
On dispose de deux baguettes et d'un madrier de section carrée, et on désire creuser dans le sol un tranchée de section demi-circulaire.
La figure Cerclci5.fig permet de montrer la méthode. Le déplacement du sommet inférieur associée au lieu géométrique du mêmesommet inférieur permet de résoudre le problème.