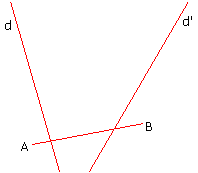
On donne deux droites d et d’ et un segment [AB].
Construire un point E de d’ et un point F de d tels que le quadrilatère ABEF soit un parallélogramme.
| Un problème de construction mobilisant une translation |
| Équipe académique mathématiques Bordeaux, juin 2002 |
Fiche élève partie I
(distribuée en début de séance)
Enoncé
| On donne deux droites d et d’ et un segment [AB]. Construire un point E de d’ et un point F de d tels que le quadrilatère ABEF soit un parallélogramme. |
|
Fiche élève partie II
(distribuée après la séquence orale utilisant l’imagiciel)
1. Construire à la règle et au compas la droite d’’ translatée de
la droite d dans la translation de vecteur 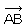 . On laissera apparents les
traits de construction.
. On laissera apparents les
traits de construction.
2. Soit E le point d’intersection des droites d’ et d’’.
Construire le point F tel que le quadrilatère ABEF soit un parallélogramme.
3. Démontrer que le point F appartient à la droite d.
En déduire que le parallélogramme ABEF répond à la demande.
4. Les questions précédentes nous ont permis d’aboutir en construisant d’abord le point E puis le point F.
Proposer une méthode qui amène à construire le point F puis le point E.
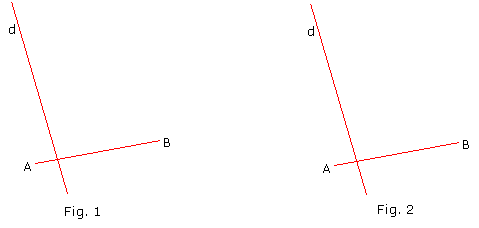
5. Construire :
Fig 1 : une droite d’ telle que la construction demandée soit impossible (même en sortant du cadre).
Fig 2 : une droite d’ telle que plusieurs parallélogrammes répondant à la demande existent.
Séquence de travail à l’oral utilisant l’imagiciel
| 1. Ecran initial Il montre les droites d et d’ et le segment [AB]. Dans le but de rappeler la notion de translation en l’illustrant de façon dynamique, il peut s’avérer pertinent “d’oublier” un instant la configuration initiale pour ne retenir que le segment [AB] et visualiser des parallélogrammes ayant [AB] comme côté … |
|
| 2. Commande 0 : Fait disparaître les droites d et d’ (commande bascule). Commande V : (le point F est pilotable à la souris). Commande P : Crée le parallélogramme ABEF. La possibilité de déplacer le point F et de disposer de son image E dans la translation de vecteur tout en montrant (ou non) le parallélogramme sous-jacent “ancre” une image mentale dynamique de la translation réutilisable ultérieurement. Commande A (ou Commande B) : Replace les points F et E respectivement sur A et B. On peut alors revenir au problème initial et proposer
à un élève de tenter “d’ajuster” le vecteur Après quelques hésitations, l’idée de faire “glisser” le point F sur d et “d’ajuster” le seul point E sur d’ vient naturellement … |
|
| 3. Commande CTRL F : Crée une poignée verte pilotable à la souris sur la droite d. Commande F : Affecte le point F sur la poignée. Le point F est alors assujetti à se déplacer sur d. (La commande L libère, si on le souhaite, le point F de cette contrainte et le rend de nouveau pilotable à la souris dans le plan tout entier). Commande Trace : Affiche la trace du point E lors des essais d’ajustement. En s’interrogeant sur la définition de chaque point de cette trace, on s’attachera à faire émerger de notre démarche pragmatique l’intérêt de la construction de l’image de la droite d dans la translation de vecteur . |
|
| 4. Commande d : Droite d’’ translatée de d dans la translation de vecteur
Commande 1 : Affecte E au point d’intersection de d’ et d’’. Après cette activité de recherche menée à l’oral, on peut proposer la partie II de la “ fiche élève ” qui demande la réalisation de la construction à la règle et au compas ainsi que la mise en forme du raisonnement. Les commandes décrites ci-dessous proposent une illustration
de la question 4 de la “ fiche élève ” : On utilise ici
la translation de vecteur 5. Commande CTRL V : Crée un vecteur Commande CTRL P : Crée le parallélogramme ABE’F’. |
|
| Commande A (ou Commande B) : Replace les points F’ et E’ respectivement sur A et B. Commande CTRL E : Crée une poignée rouge pilotable à la souris sur la droite d’. Commande E : Affecte le point E’ sur la poignée. Le point E’ est alors assujetti à se déplacer sur d’. (La commande L libère, si on le souhaite, le point E’ de cette contrainte et le rend de nouveau pilotable à la souris dans le plan tout entier). Commande Trace : Affiche la trace du point F’ lors des essais d’ajustement. Cette démarche amène à construire l’image de la droite d’ dans la translation de vecteur etc … Commande CTRL d : Droite d’’’ translatée de d’ dans la translation de vecteur
Commande 1 : Affecte F’ au point d’intersection de d et d’’’. |
|