| Droites particulières d'un triangle |
|
Collège F. Pécaut 64 Salies de Béarn
Bordeaux, Groupe Math&info 93/94 |
|
|
Niveau
5e, 4e.
Objectifs
Familiariser l’élève avec les droites particulières d'un triangle.
Explorer une figure et approfondir les connaissances.
Prérequis
Maîtrise des notions de milieu de segment, droite perpendiculaire,
angle, axe de symétrie, médiatrice d'un segment, bissectrice d'un angle, triangle,
côtés, sommets.
Connaissance des définitions et des constructions de la hauteur d'un triangle
et de la médiane d'un triangle (en tant que droites), ou, au moins, les avoir
sous les yeux.
Bonne pratique de Cabri-Géomètre.
Organisation pratique
Logiciel : Cabri Géomètre.
Un PC pour un ou deux élèves avec fiche de directives et questionnaire
Système de rétroprojection.
Description
La séance a pour but de montrer (et non de démontrer !)
qu'en général, hauteur, médiane, médiatrice et bissectrice sont des droites
différentes, que le seul cas où deux d'entre elles sont confondues est le cas
du triangle isocèle et que, dans ce cas, les quatre droites sont confondues.
Dans les trois premières parties (médiatrice, hauteur et médiane)
les preuves sont assez simples à trouver et la rédaction attendue peut se limiter
aux réponses aux questions (1/2 h en dirigé, 1 h en autonomie selon le niveau
des classes).
La quatrième partie (la bissectrice) est mieux exploitée sous
la direction du professeur en interactivité avec la classe (tablette rétroprojetable).
On se contentera d'observer et de conjecturer (pas plus de 20 min installation
comprise).
Bilan
Cette séance ne remplace pas un séance de construction sur papier
avec les instruments de mesure.
La quatrième partie, explorée assez maladroitement par les élèves,
a été reprise avec tablette rétrojetable la fois suivante et le message est
bien passé.
Préliminaire
1. Lancer Cabri-Géomètre.
2. Créer un triangle, nommer ses sommets A, B, C. Mesurer ses
côtés.
3. Construire le milieu de [BC], le nommer M.
Médiatrice
Construire la médiatrice de [BC]. La nommer (D).
En déplaçant les sommets, vérifier que A n'est pas obligatoirement sur (D) mais
que M est bien toujours sur (D).
Que semble devenir ABC lorsque l’on place A sur (D) ?
Pourquoi peut-on être sûr qu'il en est bien ainsi ?
Hauteur
Enlever A de (D).
Construire la hauteur de ABC relative à A (droite perpendiculaire à [BC] passant
par A) et vérifier que cette hauteur n'est pas la médiatrice (D).
Déplacer A.
Pourquoi peut-on dire avec certitude que cette hauteur et la médiatrice de [BC]
sont parallèles ?
Où doit être A pour que ces deux droites soient confondues ?
Que devient alors le triangle ABC ?
Si le triangle ABC n'est pas isocèle, la hauteur relative à A peut-elle passer
par le milieu M du côté opposé ?
Médiane
Enlever A de (D).
Construire la médiane de ABC relative à A (droite définie par les points A et
M).
Vérifier qu'on obtient une droite encore différente des deux autres.
Colorier ces trois droites avec des couleurs différentes pour bien les distinguer.
Si le triangle ABC n'est pas isocèle, pourquoi la médiane ne peut pas être confondue
avec la hauteur relative à A ? (penser à M)
Si le triangle ABC n'est pas isocèle, pourquoi la médiane ne peut pas être confondue
avec la médiatrice de [BC] ? (penser à A)
Que peut-on affirmer avec certitude si on sait qu'une médiane est confondue
avec une médiatrice ou bien avec une hauteur ?
Bissectrice
Veiller à ce que A ne soit pas sur (D).
Construire la bissectrice de l’angle 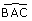 et vérifier qu'on obtient
encore une autre droite différente des précédentes.
et vérifier qu'on obtient
encore une autre droite différente des précédentes.
Si A n'est pas sur (D), (D) est-elle axe de symétrie de 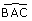 ?
?
Si le triangle ABC n'est pas isocèle en A, la médiatrice de [BC] et la bissectrice
de 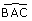 peuvent-elles être confondues ?
peuvent-elles être confondues ?
La bissectrice de 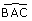 semble-t-elle pouvoir passer
par M ? Quand ?
semble-t-elle pouvoir passer
par M ? Quand ?
Si le triangle ABC n'est pas isocèle en A, que penser de la médiane relative
à A et de la bissectrice de 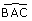 ?
?
La bissectrice de 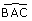 semble-t-elle pouvoir être
sans point commun avec la médiatrice de [BC] ? Semble-t-elle pouvoir être perpendiculaire
à [BC] ? Quand ?
semble-t-elle pouvoir être
sans point commun avec la médiatrice de [BC] ? Semble-t-elle pouvoir être perpendiculaire
à [BC] ? Quand ?
Si le triangle ABC n'est pas isocèle en A, que pensez-vous de la hauteur relative
à A et de la bissectrice de 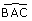 ?
?
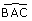 et vérifier qu'on obtient
encore une autre droite différente des précédentes.
et vérifier qu'on obtient
encore une autre droite différente des précédentes.