Niveau

Classe de quatrième

Objectifs

Mettre en évidence la position du centre de gravité dans un triangle.

Prérequis

L'ensemble de la classe est déjà familiarisé avec l'utilisation de "Cabri-Géomètre" et en particulier l'élève qui est au clavier et effectue les manipulations qu'on lui demande ainsi que l'historique de la construction à la demande.

Organisation pratique

Ordinateur "Tableau noir" : un PC + tablette à rétroprojeter et le logiciel "Cabri-Géomètre".
Instruments de dessin et de mesure pour les élèves.

Description

Durée  : environ trois quarts d'heure.
Il s'agit de conduire à l'écran la démonstration classique de la position du centre de gravité dans le triangle avec ces deux avantages :
q     un élève étant au clavier, le professeur a les mains libres et est plus disponible pour observer et répondre aux questions
q     possibilité d'animer la figure pour observer les cas particuliers qui parfois posent quelques petits problèmes aux élèves et sont souvent très intéressants.

Bilan

Le fait de ne pas avoir de figure à dessiner au tableau et donc de pouvoir toujours regarder les élèves permet d'éviter leur bavardages.
Participation active des élèves.

Déroulement du cours

1. On commence par rappeler la définition de la médiane dans un triangle et la copier.

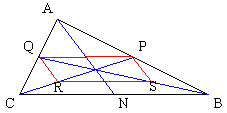
2. On trace un triangle quelconque ABC et les milieux respectifs N, P, Q des côtés [BC], [AC], [AB] du triangle.
Afin de garder la figure claire on ne trace que les médianes [BP] et [CQ] sécantes en G.
On appelle R et S les milieux respectifs de [BG] et [CG] et l'on trace le quadrilatère PQRS .....et on attend les plus lents. Il est vrai que cette construction est particulièrement rapide avec ce logiciel.
Qu'évoque pour vous le mot "milieux" dans un triangle ? .......La droite des milieux !
Quelle semble être la nature du quadrilatère PQRS ?......Un parallélogramme !

3. On passe en revue les propriétés réciproques du parallélogramme et on retient qu'il faut s'intéresser aux droites (PQ) et (RS) et peut-être aux segments [PQ] et [RS] parce que certains ont bien vu les deux triangles ABC et BGC celui-ci ne sautant pas aux yeux ! Deux élèves voudraient que l'on trace (AG)... Ils pensent (sans doute avec raison que ce serait plus facile  !) et pour les calmer je leur dis qu'ils proposeront leur démonstration après la nôtre...!

Rapidement on s'aperçoit que les droites (PQ) et (RS) sont parallèles toutes les deux à (BC) et les côtés [PQ] et [RS] ont pour mesure la moitié de [BC] en observant les deux triangles ci-dessus et en utilisant la propriété de la droite des milieux.

Par conséquent PQRS est bien un parallélogramme. La parole est alors donnée à l'un des deux élèves qui propose une excellente démonstration aussi souvent utilisée d'ailleurs mais je passe !

On retient donc que les diagonales se coupent en leur milieu et que si RG = GP et RG = RB par construction  alors les trois segments [RB] [RG] [GP] ont la même mesure, d'où la position bien particulière du point G sur cette médiane [BP]. Un élève se propose de montrer qu'il en est de même de la place de G sur la médiane [CQ] et qu'il en serait de même de G sur [AM].

4. On trace alors un second triangle abc à l'écran avec ses trois médianes et on vérifie que ga = 4,8 et gm = 2,4 et que par conséquent le centre de gravité est situé sur chaque médiane aux deux tiers à partir du sommet.

5. On ne s'attarde pas sur le triangle isocèle ni sur le triangle équilatéral et pas plus sur le triangle rectangle mais on constate tout de même que dans certains cas le quadrilatère PQRS est  un rectangle, un losange ou un carré. Alors on sauvegarde la figure et on en reparlera sans doute car il se fait tard !