| Centre de gravité d'un triangle : une étude de
lieu |
|
Équipe académique Mathématiques
Bordeaux, novembre 2003 |
|
|
Niveau
Classe de quatrième
Objectifs
Initiation à la notion de lieu.
Travail sur les droites remarquables du triangle, en application
de la propriété du centre de gravité situé aux 2/3 de la médiane (celle-ci n'est
pas une compétence exigible du programme mais peut être vue).
Prérequis
S’il veut utiliser l'imagiciel tout prêt, le professeur doit
avoir quelques notions sur les logiciels de géométrie dynamique et être familiarisé
avec les commandes élémentaires de Géoplan.
S’il veut "fabriquer" ou adapter le fichier lui-même,
le professeur doit avoir une bonne maîtrise de Géoplan.
Aucun prérequis informatique pour les élèves : c’est le
professeur qui utilise le logiciel.
Par contre les élèves doivent connaître :
- les propriétés du parallélogramme (ici les diagonales qui se
coupent en leur milieu) (vu en 5e)
- le cercle comme ensemble de points équidistants d'un point
donné (vu en 6e)
- les médianes d'un triangle, leur concourance et la position
du centre de gravité au 2/3 sur chaque médiane (vu en 4e)
- il sera utile qu'ils aient travaillé sur les fractions si on
veut rédiger correctement et montrer que OG = 1/3 OM.
Les élèves n'ont pas vu les vecteurs mais cela n'est pas nécessaire
pour la démonstration.
Organisation pratique
Utilisation en classe entière avec un ordinateur relié à un vidéo-projecteur.
Logiciel Géoplan + fichier gravlieu.g2w.
Description
Activité de recherche.
Le professeur manipule l’imagiciel créé avec Géoplan au fur et à mesure de l’avancement de la séance.
Durée approximative de la séance :
1 heure pour la recherche progressive et la formulation
de la conjecture
puis rédaction de la démonstration (qui peut par exemple
être faite en dehors de la classe sur la base de notes prises en classe)
Énoncé de l’exercice
| Sur la figure ci-contre,
C est un cercle de centre O. Le
point A est fixe sur ce cercle, et le point M est mobile sur ce même cercle.
On définit le point B tel que le quadrilatère OAMB
soit un parallélogramme.
Le point G est le centre de gravité du triangle OAB.
Quel est l’ensemble des points que décrit G quand
M se déplace sur le cercle ? |

|
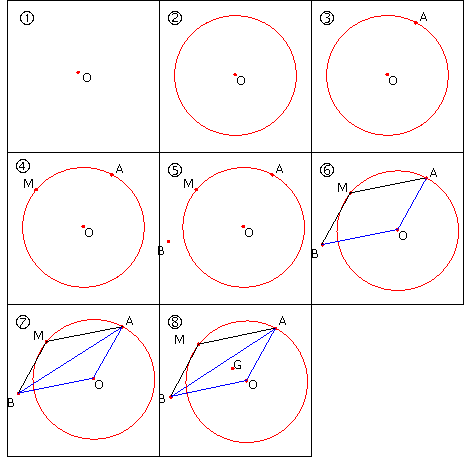
Construction de la figure
La touche A permet de tracer la figure
pas à pas devant les élèves :
La conjecture
| Il faut amener les élèves
à formuler des conjectures qui pourront être vérifiées à l’aide du logiciel.
Par exemple en visualisant la trace laissée par le
point G quand on déplace le point M sur le cercle.
La touche G permet de
garder la trace du point G.
La touche M permet de
déplacer le point m sur le cercle à l’aide des flèches de direction.
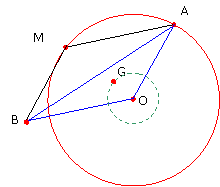
"Le point G semble décrire un cercle dont on
peut chercher à exprimer le rayon." |
|
Questionnement et conjectures intermédiaires
On pourra compléter la figure afin de pouvoir énoncer des conjectures
intermédiaires :
| "M, G et O sont alignés"
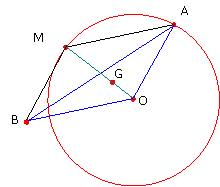
|
Pour le démontrer on construit
le point I
![Construction du milieu I de [AB]](gravlieu05.gif)
|
Passage à l’écrit
Il reste ensuite à dégager les étapes successives de la démonstration
et à la rédiger.




![Construction du milieu I de [AB]](gravlieu05.gif)