Dessine un segment [AB] de 5 cm en bleu (loin des bords de l'écran).
Place un point M et dessine les segments [MA] et [MB].
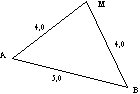
Trouve une position du point M pour que [MA] et [MB] mesurent chacun 4 cm.
La médiatrice et ses délices |
| Collège Félix Pécaut, Salies de Béarn |
Niveau
Classe de sixième
Liaison avec le programme
Vocabulaire mathématique mis en œuvre dans des consignes à exécuter.
Manipulation d’objets géométriques et observations.
Objectifs
Découverte ou redécouverte d'un environnement : celui de la médiatrice d'un segment.
Prérequis
Connaissance du vocabulaire de base de la géométrie.
Point, segment, droite, milieu, distance, ...
Connaître les commandes ordinaires du logiciel Cabri-Géomètre pour Windows
Organisation pratique
En atelier informatique, deux élèves par poste.
Logiciel Cabri-Géomètre pour Windows.
Les élèves ont un cahier d'essais.
Description
Deux séances de une heure.
Les élèves travaillent en autonomie. Ils sont guidés par la fiche distribuée et le professeur qui intervient sur un poste (un poste relié à un téléviseur en hauteur).
Bilan
Les élèves apprécient d'aller en atelier informatique. "On n'a pas l'impression de travailler...."
Pourtant c'est bien là qu'ils sont le plus attentif aux consignes et aux résultats qu'ils obtiennent !
Après cette séance les élèves associent davantage d'environnement et de sens au mot "médiatrice".
Remarque
Ces travaux individuels peuvent utilement faire suite à la séance "Découverte de la médiatrice", collective avec le même logiciel et une tablette à rétro-projeter.
Première partie
| Dessine un segment [AB] de 5 cm en bleu (loin des bords de l'écran). Place un point M et dessine les segments [MA] et [MB]. Trouve une position du point M pour que [MA] et [MB] mesurent chacun 4 cm. |
|
Peux-tu, après avoir trouvé cette position, en trouver une autre pour la même consigne ?
Déplace le point B pour que [AB] mesure maintenant 9 cm.
Peux-tu retrouver une position du point M pour qu'il soit encore à 4 cm de A et de B ?
Est-il possible de placer M à 6 cm de A et de B ?
Rapproche M le plus possible du segment [AB] tout en veillant à maintenir la longueur MA égale à la longueur MB. (Attention les mesures ne sont précises qu'au mm près).
Quel est le trajet du point M ?
Pour quelle position de M la distance MA (égale à la distance MB) est-elle la plus courte ?
Deuxième partie
Avec un compas
| Efface tout. Dessine un segment près du bord de l'écran et mesure le (ce sera l'ouverture du compas). Place un point A et un point B Dessine le cercle de centre A avec le rayon choisi (Construction Compas). Dessine le cercle de centre B en choisissant le même rayon. |
|
Choisis une ouverture de compas pour que les cercles soient sécants.
Désigne par E et F les points d'intersection des deux cercles. Donne leur la couleur rouge.
Explique pourquoi E est équidistant de A et de B. Et pour F ?
Modifie l'ouverture du compas (plus grande, puis plus petite, et même très petite !) Observe pour quelles valeurs du rayon les points E et F n’existent pas..
Rends les deux cercles invisibles (Aspect Cacher/montrer)
Dessine en vert les segments [EA], [EB], [FA], [FB], et mesure-les. Est-ce surprenant ?
Quelle est la forme du quadrilatère de couleur verte ?
Agis encore sur l'ouverture du compas et observe les déplacements de E et de F.
Pour garder la trace des déplacements, cliquer sur trace dans le menu Affichage, clique sur E puis sur F qui doivent alors clignoter.
Agis ensuite sur l'ouverture du compas en l’augmentant ou en la diminuant.
Qu'observes-tu à propos de la trace laissée en rouge par ces deux points ?
Recommence avec d'autres longueurs pour le segment [AB].
Efface le lieu obtenu (Ctrl F ou option Tout redessiner du menu Edition) .
Construis le milieu du segment [AB] (Construction milieu).puis la perpendiculaire au segment [AB] en son milieu (Construction Droite perpendiculaire). Cette droite contient les points E et F.
Vérifions cela
| Efface tout. Dessine [AB] en bleu et son milieu K en rouge (Construction milieu) Dessine en rouge la droite (D) perpendiculaire au segment [AB] en son milieu. (Construction Droite Perpendiculaire) Place un point E sur (D) (Construction Point sur objet). Compare les mesures des segments [EA] et [EB]. Que remarques-tu lorsque tu déplaces le point E sur (D) ? |
|
Conclusion
Tous les points équidistants de A et de B forment une droite qui coupe le segment [AB] perpendiculairement en son milieu.
Tous les points de la droite qui coupe le segment [AB] perpendiculairement en son milieu sont équidistants de A et de B
Cette droite est appelée la médiatrice du segment [AB].
Le Menu Construction dispose de la commande qui permet de tracer immédiatement cette droite dès que l'on connaît le segment ou seulement ses extrémités.
Entraîne toi
Efface tout. Place 4 ou 5 points sur l'écran.
Imagine la médiatrice de deux d'entre eux, puis construis la pour vérifier.
(Construction Médiatrice)
Décris sur ton cahier deux méthodes, l'une au compas, l'autre avec une règle graduée et l'équerre pour construire la médiatrice du segment [AB].
Un cadeau de la médiatrice
| Efface tout. Dessine un triangle ABC en bleu (Lignes Triangle) Construis la médiatrice du côté [AB] puis celle du côté [BC] Désigne par O le point d'intersection des deux médiatrices. (Construction Intersection de deux objets) |
|
Donne lui la couleur rouge.
Rends invisibles les médiatrices.
Dessine les segments [OA], [OB], [OC], en vert.
Mesure les 3 segments de couleur verte.
Pouvais-tu prévoir cette particularité ?
Dessine le cercle de centre O qui contient le point A (Courbes Cercle )
Il contient bien sûr les deux autres sommets du triangle.
Ce cercle est appelé cercle circonscrit au triangle ABC.
Dessine la médiatrice du troisième côté [AC] du triangle.
Explique pourquoi elle contient le point O.
Retiens
Les médiatrices des trois côtés d'un triangle sont concourantes
Leur point de concours est le centre du cercle circonscrit au triangle.
As-tu bien compris ?
| Fais une figure qui montre un triangle de couleur bleue, son cercle circonscrit de couleur verte, le centre de ce cercle en rouge et rien d'autre ! Déplace les sommets du triangle et observe que le centre du cercle circonscrit est parfois intérieur au triangle, parfois extérieur et parfois sur un des côtés (dans ce cas, il en est le milieu !). |
|