Niveau

Classe de sixième

Liaison avec le programme

Exploitation du vocabulaire mathématique.
Conjecturer, vérifier.
Utilisation d’objets variables pour observer des propriétés invariantes.
Définition de la médiatrice

Objectifs

Découvrir la médiatrice d'un segment d'une façon dynamique.

Prérequis

Connaissance du vocabulaire de base de la géométrie (point, segment, droite, distance, milieu, perpendiculaire).
Le professeur connait bien le logiciel Cabri-Géomètre pour Windows.
Les élèves ont déjà assisté à des séances de travail utilisant un ordinateur et une tablette rétroprojetable (ils ont dépassé le stade de la surprise et peuvent se concentrer sur le sujet traité.)

Organisation pratique

Salle de classe avec un PC et une tablette sur un rétroprojecteur (Le tout, par exemple, sur un chariot.).ou une liaison PC - TV.
Le logiciel Cabri-Géomètre pour Windows. Les élèves ont leur matériel habituel.

Description

Durée : une séance de cours.
l En interaction avec la classe, le professeur anime la séance, manipule les commandes et valide les découvertes.
l Les élèves prennent des notes sur leur cahier d'essais (brouillon), font des figures sur les conseils du  professeur.

Bilan

Réaction d’élèves : "C'est super ! On pourra en refaire ?"
Cette réflexion spontannée et non isolée est un puissant moteur pour multiplier les séances.
La facilité de reproduire des situations ou de les modifier d'une façon continue permet au professeur de focaliser la curiosité et d'entretenir l'intérêt des élèves.
La très bonne participation de la classe est aussi l'occasion de mettre à jour le vocabulaire et de remplacer une gestuelle par une phrase.
En fin de séance, la médiatrice existe, les élèves l'ont rencontrée ! Les références à ces figures qui bougent sont précieuses en géométrie "craie-tableau" où le "vu" prend le pas sur le "su".

Des travaux individuels sont proposés sur ce même sujet et peuvent utilement faire suite à cette séance : "La médiatrice et ses délices"

La séance

On dispose d'une "provision" de points que l'on crée et que l'on nomme. Cette réserve, dans un coin de l'écran, sera exploitée selon les besoins.

Deux points de base A et B sont placés. Un point M est déplacé sur l'écran.
Comparer visuellement les distances MA et MB.

Tracer [MA] et [MB], les mesurer, déplacer le point M, observer.(les mesures, avec une décimale, restent apparentes et suivent les segments).
Rendre invisibles ces deux segments.

Estimer des positions de M pour lesquelles MA et MB semblent égales. (participation de la classe, vocabulaire "équidistant").

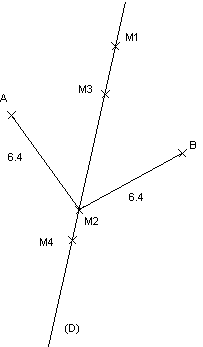
Puiser dans la réserve les points M₁, M₂, M₃, ... qui occuperont ces positions.

Vérifier en faisant réapparaître les segments [MA] et [MB] et en plaçant M sur chacune de ces positions. (Attribuer un prix de précision à 0,1 près et corriger les positions des points M_i)

Remarque

À ce niveau, la gestion des ambiguïtés est l'occasion de faire la distinction entre un point placé Mi et le point courant M. Faire des observations sur la position des points équidistants de A et de B. Vérifier l'alignement par référence à une droite que l'on déplace comme une règle (cf. annexe). Les autres points de cette droite (D) ainsi positionnée sont-ils équidistants de A et de B ? Pour y répondre lier le point M à la droite (D) et constater que lorsque M parcourt (D) MA et MB restent égales.(il faut là sacrifier un peu de rigueur...)

Avec un compas

Effacer tout.
On aura besoin d'un segment sur un bord de l'écran pour l'écartement du compas
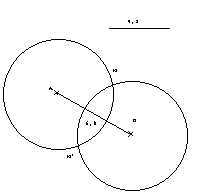
Dessiner les points de base A et B et deux cercles de même rayon et de centres A et B.
Choisir un rayon suffisant pour définir et nommer leurs points d'intersection M et M'.
Constater leur disparition lorsque le rayon devient trop petit (agir sur la longueur du segment).

Récolter les commentaires.
Rayon mini : que se passe-t-il ?

Tracer [MA] et [MB], mesurer : M est équidistant de A et de B (bien sûr !).

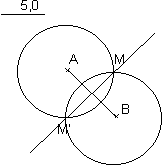
	Tracer [AB]. Trouver le plus petit écartement qui maintienne l'existence des points M et M'. Présence du milieu de [AB].
	Construire le lieu des points M et M' lorsque le rayon varie. (Sélectiuon avec l’option trace du menu Aspect puis Animation). Admirer et recommencer pour d'autres positions des points A et B.

Observations à noter sur le cahier d’essais

• Tous les points équidistants de A et de B sont alignés.
• La droite formée de tous les points équidistants de A et de B est appelée la médiatrice du segment [AB].
• La médiatrice contient le milieu du segment.
• Pour tracer la médiatrice d'un segment, deux points obtenus avec le compas suffisent.

C'est le moment de faire plusieurs constructions sur le cahier.

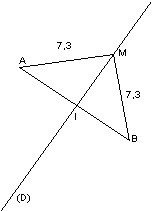Le segment et sa médiatrice semblent être perpendiculaires. Construire un segment [AB]. Construire son milieu avec la commande Cabri. Construire la perpendiculaire (D) au segment en son milieu avec la commande Cabri. Construire M sur (D) et mesurer les segments [MA] et [MB]. Déplacer M lié à (D).

Conclusion

La médiatrice d'un segment est la droite formée de tous les points équidistants des extrémités du segment

La médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu.