Niveau

Cinquième, quatrième.

Objectifs

Faire découvrir aux élèves les parallélogrammes particuliers, rectangle, losange, carré, ainsi que les propriétés de ces figures.

Prérequis

Connaitre les propriétés du parallélogramme

Organisation pratique

Une salle équipée d'un ordinateur et d'une tablette rétro-projetable. Le logiciel Cabri-Géomètre II.

La précision des mesures pose ici un problème. Il est pratiquement impossible de faire marquer l’angle droit comme on a l’habitude de le faire. Pour limiter les problèmes, il vaut mieux,dès le départ diminuer la précision et demander 0 chiffre après la virgule pour les angles et un seul pour les longueurs.

Pour accélérer les manipulations, le professeur doit avoir, au préalable, défini un certain nombre de macro-constructions :

* Parallélogramme permet, à partir de 3 points A, B, C, de tracer le parallélogramme A,B,C,D.
* Diagonales+angles permet de tracer les diagonales et de marquer l'angle de ces diagonales.
* Diagonales+longueurs permet de tracer les diagonales et de mesurer leurs longueurs.
* Demi-diagonales permet de tracer le point d'intersection des diagonales, les segments joignant ce point aux 4 sommets du parallélogramme et les longueurs de ces segments.

Le professeur crée égalament trois fichiers : rectangle.fig, losange.fig et carre.fig

Durée : 1 heure.

Description

Les éléves doivent, à partir d'un parallélogramme quelconque, trouver toutes les positions particulières.

La séquence se déroule en deux temps. D'abord, à partir d'un parallélogramme, on cherche à obtenir le rectangle, le losange et le carré. Les élèves viennent manipuler à tour de rôle.

Dans un deuxième temps, à partir des figures rectangle.fig, losange.fig et carre.fig et des macros précédentes on pourra retrouver les propriétés de ces figures.

Les figures obtenues sont ensuite reproduites par les élèves sur des feuilles non quadrillées à l'aide des instruments de géométrie habituels.

Bilan

Les manipulations ont été effectuées par des élèves qui ont davantage participé que si la même leçon avait été réalisée de façon classique.

L'ordinateur permet de découvrir ces positions particulières par tatonnement et élimine les problèmes de constructions nécessaires à l'obtention de ces parallèlogrammes particuliers.

D'autre part, les élèves comprennent plus facilement que ces nouvelles figures sont toutes des parallélogrammes avec "quelque chose en plus".

Les reproductions sur papier de ces figures sont facilitées par le fait que les élèves ont sous les yeux la figure qu'ils doivent obtenir.

Enfin, les élèves sont plus motivés pour la suite de la leçon.

Document professeur

Penser à modifier la précision de l’affichage pour limiter les problèmes. Si, lors des manipulations, on arrive à un parallélogramme ayant 2 côtés consécutifs perpendiculaires (ou marqués comme tels) et dont les diagonales n’ont pas la même  longueur, ce sera l’occasion de parler de la précision des mesures…

Le parallélogramme

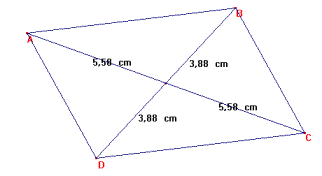Cette première activité permet de rappeler les propriétés des parallélogrammes. On dispose au départ d'un parallélogramme quelconque. On mesure les 4 segments crées par la macro Demi-diagonales et vérifie ainsi que les diagonales se coupent en leur milieu.

En utilisant la rubrique parallèle ? du menu propriété, on peut vérifier le parallélisme des côtés.
La recherche de positions particulières, faite par un élève, permet d'obtenir les trois types de parallélogrammes particuliers : le rectangle, le losange et le carré

Le Rectangle

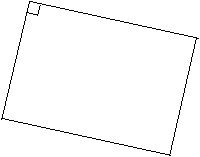On revient à la figure du parallélogramme quelconque et on cherche à obtenir une figure particulière. Par tâtonnement, et en déplaçant un des sommets mobiles, un élève arrive à une figure ayant deux côtés perpendiculaires. Quelle est la particularité obtenue ? -  Un angle droit.

On confirme en marquant (mais la marque ne sera pas la marque classique) et en mesurant cet angle (si la précision est assez faible, on peut faire afficher 90° sans trop de difficultés).

Le losange

Le point de départ est encore le parallélogramme quelconque. L'élève obtient un losange. - Pourquoi penses-tu avoir un losange ? - Les 4 côtés ont la même longueur. - Dois je mesurer les 4 côtés ? - Non, 2 mesures suffisent. - Lesquelles ? - 2 côtés consécutifs.

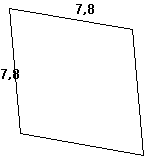Le carré

En recherchant les deux situations précédentes en même temps, on obtiendra le carré. Pour obtenir un carré, il suffit, à partir du parallélogramme d'avoir, en plus, deux côtés consécutifs de même longueur et perpendiculaires.

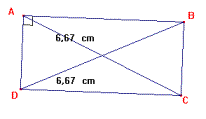
Étude des propriétés du rectangle

Charger la figure Rectangle.fig. Constater que, ici, la marque de l’angle de 2 côtés consécutifs est bien la marque habituelle de l’angle droit. En utilisant la macro Diagonales+longueurs , on peut vérifier que les diagonales ont la même longueur. En faisant varier les sommets, on pourra vérifier que cette propriété reste vraie pour tout rectangle. On pourra aussi mesurer les 3  autres angles du rectangle et vérifier qu'ils restent tous droits même en modifiant la figure.

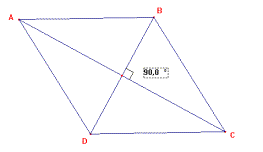
Étude des propriétés du losange

À partir de la figure losange.fig, on pourra à l'aide de la macro Diagonales+angles, vérifier que les diagonales sont orthogonales, puis en mesurant les côtés vérifier que les 4 côtés ont même longueur

Étude des propriétés du carré

À partir de la figure carre.fig, et en refaisant successivement les manipulations faites pour le rectangle et pour le losange, on retrouvera les propriétés des carrés.

Document élève

Cette fiche sera complétée par les figures que vous avez reproduites pendant la séquence en salle informatique.

Parallélogramme

Tout parallélogramme a ses côtés parallèles deux à deux.
Tout parallélogramme a des diagonales qui se coupent en leurs milieux.

Rectangle

Un rectangle est un parallélogramme qui a, de plus, deux côtés consécutifs perpendiculaires.
Tout rectangle a 4 angles droits.
Tout rectangle a des diagonales de même longueur.
Tout rectangle a bien sûr toutes les propriétés des parallélogrammes.

Losange

Un losange est un parallélogramme qui a, de plus, deux côtés consécutifs de même longueur.
Tout losange a ses 4 côtés de même longueur.
Tout losange a des diagonales perpendiculaires.
Tout losange a, bien sûr, toutes les propriétés des parallélogrammes.

Carré

Un carré est un parallélogramme qui a, de plus, deux côtés consécutifs perpendiculaires et de même longueur.
Tout carré a 4 angles droits.
Tout carré a 4 côtés de même longueur.
Tout carré a des diagonales perpendiculaires.
Tout carré a des diagonales de même longueur.
Tout carré a, bien sûr, toutes les propriétés des parallélogrammes.