Propriétés des rectangles |
|
| Collège Félix Pécaut, Salies de Béarn
Groupe Math&Info, Bordeaux, 95/96 |
|
|
Niveau
Sixième.
Liaison avec le programme
Symétrie axiale. Rectangle, vocabulaire.
Objectifs
Révision des connaissances du CM sur les propriétés des rectangles.
Exploration de figure et approfondissement de ces connaissances.
Prérequis
Pour les élèves : Connaissance des définitions et des
constructions : rectangle et vocabulaire associé, symétrie orthogonale,
Pour le professeur : Bonne pratique de Cabri-Géomètre
Modalités d'utilisation
Logiciel : Cabri Géomètre + quelques figures simples préparées
à l'avance, plus pour ne pas éparpiller l'attention que pour gagner du temps
: rectang1.fig à rectang5.fig
Tablette rétro + rétroprojecteur. Ou liaison PC-TV
Description
La séance (une heure) a pour but de faire s'exprimer les élèves
et de dresser un bilan des propriétés.
Le professeur anime les figures et dialogue avec (et fait dialoguer) la classe.
De temps en temps, il note au tableau une propriété.
Leur réponses sont éventuellement corrigées, si possible par les autres élèves.
Cette séance est aussi l'occasion de casser certaines images trop prégnantes
sur la forme ou la position des rectangles et d'insister sur le fait qu'un carré
est un rectangle.
Bilan
Beaucoup d'animation dans la classe oł chacun veut s'exprimer
sur un sujet qu'il connaît bien. Le professeur doit écouter et contrôler les
débats et s'occuper de la figure
Auteur
Collège F. Pécaut 64 Salies de Béarn
Bordeaux, Groupe Math&info 95/96
Mise à jour Math&Info2001/2002
LES RECTANGLES
Figure RECTANG1.FIG
- Qu'est-ce que c'est ?
- Un rectangle à côtés horizontaux et verticaux avec leurs mesures.
- Qu'en faire ?
- Le déformer, le faire vivre.
Montrer (au sens de faire voir) que, même ainsi "posé", la longueur
n'est pas obligatoirement le côté horizontal.
Montrer que, dans la profusion de rectangles qu'on est amené à manipuler,
certains ont des côtés de même longueur. Un rectangle peut être un carré.
Figure RECTANG2.FIG
- Qu'est-ce que c'est ?
- Un rectangle à côtés quelconques avec leurs mesures et avec des angles marqués.
- Qu'en faire ?
- Le déformer, le faire tourner.
Montrer qu'un rectangle n'a pas obligatoirement des côtés horizontaux et verticaux.
Mais, par contre, un rectangle a des propriétés : les angles sont droits,
les côtés opposés sont de même longueur.
Construire les diagonales (segments), les mesurer.
Remarque : Certains élèves de 6ème ont retenu du rectangle une
image figée, quelque chose de stable posée sur une base, la longueur. Ils connaissent
certaines propriétés, angles droits, côtés opposés de même longueur, parallèles
car verticaux et horizontaux, ils vont en calculer le périmètre ou l'aire mais
ils sont incapables de l'admettre dans une autre position et surtout pas dans
une figure plus complexe. Ils imaginent mal un rectangle sans le support du
papier quadrillé. Il faut profiter de l'impact de l'ordinateur, objet magique
détenant la vérité, pour casser ces images tout en montrant la permanence des
propriétés.
Figure RECTANG3.FIG
- Qu'est-ce que c'est ?
- Un rectangle à côtés quelconques avec les diagonales et leur point d'intersection
et les distances de ce point aux quatre sommets .
- Qu'en faire ?
- Le déformer, le faire tourner.
Faire observer que non seulement les diagonales ont la même longueur mais
aussi le même milieu.
Faire trouver que les quatre sommets sont sur un même cercle (le construire)
et que les diagonales en sont deux diamètres.
Remarque : Vite, vite, suspendre la séance et faire construire sur
papier (tolérer le papier quadrillé) au moins deux rectangles différents et
leur cercle circonscrit.
Ensuite et sans souffler, construire, à au moins deux reprises, un cercle et
deux de ses diamètres (quelconques !). Dessiner le quadrilatère dont on a là
les deux diagonales. On a un rectangle dont les côtés ne sont ni horizontaux
ni verticaux (on n'a pas dit que c'était aussi une condition suffisante mais
en 6ème...). On a libéré le rectangle du quadrillage et on peut le libérer du
cercle en gommant ce dernier.
Figure RECTANG4.FIG
- Qu'est-ce que c'est ?
- Un rectangle ABCD, une droite et le symétrique de ce rectangle par rapport
à cette droite.
- Qu'en faire ?
- Le déplacer, le déformer.
Remarquer que le symétrique du rectangle ressemble à un rectangle.
Demander une condition pour qu'un sommet ait pour symétrique lui-même.
Demander une condition pour qu'un sommet ait pour symétrique un autre sommet.
Existe-t-il une symétrie axiale telle que A 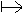 B et C
B et C 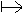 D ? Quel est l'axe de symétrie ?
Est-ce la seule qui laisse le rectangle globalement invariant ?
D ? Quel est l'axe de symétrie ?
Est-ce la seule qui laisse le rectangle globalement invariant ?
Existe-t-il une symétrie axiale telle que A 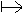 A, C
A, C 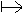 C et B
C et B 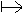 D ?
D ?
Figure RECTANG5.FIG
- Qu'est-ce que c'est ?
- Un rectangle avec les médiatrices et les milieux de ses côtés .
- Qu'en faire ?
- Rappeler que ces médiatrices sont les axes de symétrie de la figure.
Construire le quadrilatère dont les sommets sont les milieux des côtés du
rectangle.
Faire trouver (sans mesurer mais avec l'aide de la symétrie orthogonale) que
les quatre côtés de ce quadrilatère sont de même longueur. Le faire reconnaître
dans de multiples situations.
Demander si les diagonales de ce losange sont obligatoirement verticales ou
horizontales.
 B et C
B et C