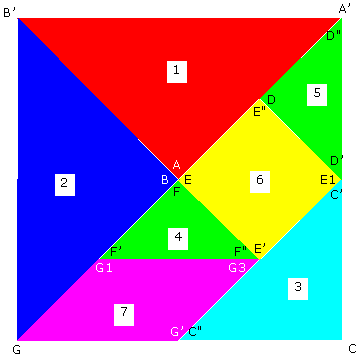
Voici le tangram à construire.
Il est constitué de sept polygones qui forment le carré A’B’GC.
Ce sont : cinq triangles rectangles isocèles, un carré et un parallélogramme.
Chacun de ces polygones doit pouvoir être déplacé indépendamment des autres.
| Tangram |
| Clg Chantaco, Saint Jean de Luz (98-99) Groupe Math&Info, Bordeaux, octobre 2002 |
Niveau
Classe de cinquième
Objectifs
En parcours diversifié, faire construire des polygones à l’ordinateur.
Prérequis
Les élèves ont déjà utilisé GéoplanW.
Déroulement
Cette activité a été réalisée dans le cadre d’un parcours diversifié « informatique et maths ».
Il faut savoir qu’un tangram est un casse-tête chinois dont le but est de composer toutes sortes de figures en utilisant obligatoirement les sept pièces du jeu.
Le livre « Secrets du tangram », éd. Gallimard jeunesse, a été apporté en classe. Il présente un tangram avec diverses possibilités de figures. Le professeur a proposé aux élèves de construire ce tangram avec Géoplan pour inventer ensuite des figures que les camarades devraient construire. Le tangram de base a été décortiqué au tableau (égalité de longueurs, angles..).
Les élèves avaient déjà pratiqué le logiciel Géoplan. Le professeur a expliqué au tableau le principe de report des longueurs en utilisant un cercle de centre et de rayon donnés.
Les menus de Géoplan n’étaient pas bridés.
Les élèves se sont lancés dans la réalisation avec une grosse difficulté pour le parallélogramme. En effet, dans un tangram, on peut retourner les pièces. Ici toutes les pièces sont identiques à la pièce retournée, sauf le parallélogramme. Ce retournement a été obtenu par une symétrie axiale et une commande de dessin en bloc.
Chacun a ensuite construit diverses figures, allant consulter le livre ou laissant libre cours à son imagination.
Bilan
Les élèves ont beaucoup apprécié cette activité. À noter qu’ils préfèrent construire leurs propres figures plutôt que celles proposées en modèle et qu’ils ont une imagination plutôt futuriste (avions, robots ou oiseaux…).
Bibliographie
L'idée de cette activité provient d’une brochure de l'Irem de Montpellier : « Activités pour la classe de sixième : nombres décimaux, aires et périmètres » n° ISBN 2-909916-24-3. Dans cette brochure les activités portent sur les aires et périmètres. Dans ce parcours diversifiés le but était de construire le tangram.
L’application pratique s’inspire d’un petit livre chez Gallimard jeunesse qui propose ce tangram ainsi que les figures qui peuvent être composées : « Secrets du tangram » (mai 1996) n° ISBN 2-07-058804-1.
Fiche élève
| Voici le tangram à construire. Il est constitué de sept polygones qui forment le carré A’B’GC. Ce sont : cinq triangles rectangles isocèles, un carré et un parallélogramme. Chacun de ces polygones doit pouvoir être déplacé indépendamment des autres. |
|
1. Sur cette figure, coder les égalités de longueurs et de mesures d’angles.
2. Vérifier que l’angle G du parallélogramme doit être égal à 45° ainsi que tous les angles aigus des triangles.
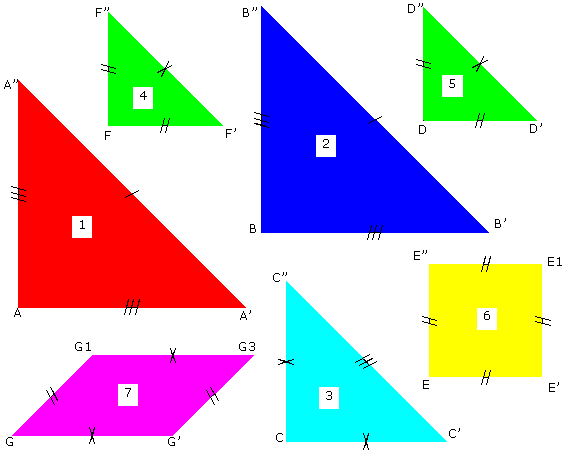
3. La figure suivante présente le tangram « éclaté ».
Construire chacun des sept polygones à l’aide du logiciel.
Attention :
Dans un tangram, les pièces doivent pouvoir être retournées.
En les retournant, les cinq triangles et le carré ne changent pas contrairement au parallélogramme.
Afin de construire le parallélogramme « retourné », il faudra construire son symétrique par rapport à la droite (GG’).
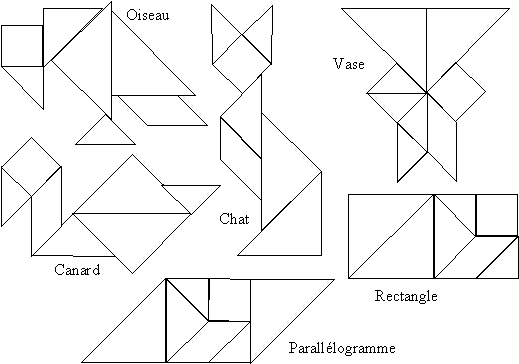
4. À l'aide des polygones précédents, réaliser les figures suivantes :
Fiche professeur
Construction du Tangram :
| a réel libre de [0,5] |
Créer, Numérique, Variable réelle libre dans un intervalle |
| A point libre |
Créer, Point, Point libre, dans le plan |
| c cercle de centre A et de rayon a |
Créer, Ligne, Cercle, Défini par centre et rayon |
| A' point libre sur le cercle c |
Créer, Point, Point libre, sur un cercle |
| d droite perpendiculaire à (AA') passant par A |
Créer, Ligne, Droite(s), Perpendiculaire |
| A" point d'intersection 1 de la droite d et du cercle c A1 point d'intersection 2 de la droite d et du cercle c |
Créer, Point, Intersection droite - cercle, 2 points |
| t1 polygone AA'A" |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| B point libre |
Créer, Point, Point libre, dans le plan |
| c' cercle de centre B et de rayon AA' |
Créer, Ligne, Cercle, Défini par centre et rayon |
| B' point libre sur le cercle c' |
Créer, Point, Point libre, sur un cercle |
| d1 droite perpendiculaire à (BB') passant par B |
Créer, Ligne, Droite(s), Perpendiculaire |
| B" point d'intersection 1 de la droite d1 et du cercle c' B1 point d'intersection 2 de la droite d1 et du cercle c' |
Créer, Point, Intersection droite - cercle, 2 points |
| t2 polygone BB'B" |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| C point libre |
Créer, Point, Point libre, dans le plan |
| c" cercle de centre C et de rayon A'A"/2 |
Créer, Ligne, Cercle, Défini par centre et rayon |
| C' point libre sur le cercle c" |
Créer, Point, Point libre, sur un cercle |
| d2 droite perpendiculaire à (CC') passant par C |
Créer, Ligne, Droite(s), Perpendiculaire |
| C" point d'intersection 1 de la droite d2 et du cercle c" C1 point d'intersection 2 de la droite d2 et du cercle c" |
Créer, Point, Intersection droite - cercle, 2 points |
| t3 polygone CC'C" |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| D point libre |
Créer, Point, Point libre, dans le plan |
| c4 cercle de centre D et de rayon AA'/2 |
Créer, Ligne, Cercle, Défini par centre et rayon |
| D' point libre sur le cercle c4 |
Créer, Point, Point libre, sur un cercle |
| d3 droite perpendiculaire à (DD') passant par D |
Créer, Ligne, Droite(s), Perpendiculaire |
| D" point d'intersection 1 de la droite d3 et du cercle c4 D1 point d'intersection 2 de la droite d3 et du cercle c4 |
Créer, Point, Intersection droite - cercle, 2 points |
| t4 polygone DD'D" |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| E point libre |
Créer, Point, Point libre, dans le plan |
| c6 cercle de centre E et de rayon AA'/2 |
Créer, Ligne, Cercle, Défini par centre et rayon |
| E' point libre sur le cercle c6 |
Créer, Point, Point libre, sur un cercle |
| d5 droite perpendiculaire à (EE') passant par E |
Créer, Ligne, Droite(s), Perpendiculaire |
| E" point d'intersection 1 de la droite d5 et du cercle c6 E2 point d'intersection 2 de la droite d5 et du cercle c6 |
Créer, Point, Intersection droite - cercle, 2 points |
| e milieu du segment [E'E"] |
Créer, Point, Milieu |
| E1 image de E par la symétrie de centre e |
Créer, Point, Point image par, symétrie centrale |
| p polygone EE'E1E" |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| F point libre |
Créer, Point, Point libre, dans le plan |
| c5 cercle de centre F et de rayon AA'/2 |
Créer, Ligne, Cercle, Défini par centre et rayon |
| F' point libre sur le cercle c5 |
Créer, Point, Point libre, sur un cercle |
| d4 droite perpendiculaire à (FF') passant par F |
Créer, Ligne, Droite(s), Perpendiculaire |
| F" point d'intersection 1 de la droite d4 et du cercle c5 F1 point d'intersection 2 de la droite d4 et du cercle c5 |
Créer, Point, Intersection droite - cercle, 2 points |
| t5 polygone FF'F" |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| G point libre |
Créer, Point, Point libre, dans le plan |
| c7 cercle de centre G et de rayon A'A"/2 |
Créer, Ligne, Cercle, Défini par centre et rayon |
| G' point libre sur le cercle c7 |
Créer, Point, Point libre, sur un cercle |
| c8 cercle de centre G et de rayon AA'/2 |
Créer, Ligne, Cercle, Défini par centre et rayon |
| G" image de G' par la rotation de centre G et d'angle 45 (degré) |
Créer, Point, Point image par, rotation (angle mesuré) |
| G1 point d'intersection 1 de la droite (GG") et du cercle c8 G2 point d'intersection 2 de la droite (GG") et du cercle c8 |
Créer, Point, Intersection droite - cercle, 2 points |
| g milieu du segment [G'G1] |
Créer, Point, Milieu |
| G3 image de G par la symétrie de centre g |
Créer, Point, Point image par, symétrie centrale |
| l polygone GG'G3G1 |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| s symétrie d'axe (GG') |
Créer, Transformation, Symétrie axiale |
| G4 image de G3 par la transformation s G5 image de G1 par la transformation s |
Créer, Point, Point image par, transformation déjà créée |
| l' polygone GG'G4G5 |
Créer, Ligne, Polygone, Polygone défini par ses sommets |
| Af0 affichage du texte: Pour retourner le parallélogramme touche R. Ouvrir en même temps un modèle. Af1 affichage du texte: Mettre les 2 figures en mosaïque. Chercher à reproduire le modèle. |
Créer, Affichage, Texte |
Afin de pouvoir retourner le parallélogramme :
Créer : Cm0 (touche R) dessin en bloc de l' (Créer, Commande, Dessin en bloc)
Appuyer une fois sur la touche R, l’ disparaît.
Créer : Cm1 (touche R) dessin en bloc de l (Créer, Commande, Dessin en bloc)
Un message apparaît : « La touche que vous avez choisie est déjà utilisée par une autre commande…» répondre oui pour grouper les commandes.
A chaque appui sur R, l ou l’ apparaîtront.