Niveau

Classe de quatrième

Objectifs

Ce qu'il n'est pas permis d'ignorer en classe de 4ème sur le triangle rectangle.

Prérequis

L'ensemble de la classe est déjà familiarisé avec Cabri-Géomètre et en particulier les élèves qui passent au clavier et effectuent les manipulations demandées ainsi que l'historique de la figure.

Organisation pratique

Ordinateur « Tableau noir » : un PC + tablette à rétroprojeter et le logiciel "Cabri-Géomètre".
Instruments de dessin pour les élèves.

Description

Durée : une heure ou moins, cela dépend du niveau de la classe.

Il s'agit de construire des triangles rectangles avec certaines contraintes. Ces constructions sont l'occasion de rappeler les propriétés à connaître en quatrième. Trois séquences correspondant aux figures TR_RECT1.FIG , TR_RECT2.FIG, TR_RECT3.FIG.

Lors de chaque séquence un élève réalise la construction avec le logiciel tandis que les autres suivent cette construction à l'écran et la réalisent sur leur cahier de cours à l'aide des instruments. A la fin de l'exercice, celui qui manipule tire le dessin sur l'imprimante et le colle dans son cahier.

Pour la dernière séquence, afin de gagner du temps, le professeur a réalisé trois triangles que l'élève pourra déplacer ou agrandir.

Bilan

Participation active et continue des élèves. Pas de temps laissé aux élèves pour le bavardage. Pas de temps perdu à tracer les figures au tableau, le dos tourné.

Rapidité des constructions. Possibilité de déplacer le point sur le cercle, de faire varier l'orthocentre...

Il s'agissait d'une révision sur le triangle rectangle. Il faudrait voir en troisième ce que les élèves en auront retenu.

Déroulement du cours

TR_RECT1.FIG

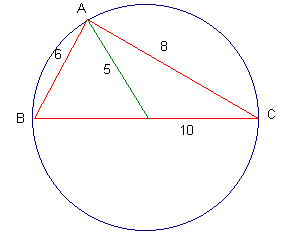
1. Construction classique d'un triangle rectangle dans un cercle de 10 cm de diamètre avec un rappel des deux propriétés recherchées par l'ensemble de la classe :

"Un triangle rectangle est inscriptible dans un cercle de diamètre l'hypoténuse"

"Lorsqu'on joint un point d'un cercle aux extrémités d'un diamètre on détermine un angle droit".

2. Chacun mesure les autres côtés de l'angle droit. A l'aide de la calculatrice on vérifie la propriété de Pythagore et on reparle de  « carré » et « racine carrée » et de mesures approchées.

3. On revient sur la définition de la médiane dans un triangle avant de construire celle relative à l'hypoténuse. On la mesure et l'on énonce la propriété de sa mesure égale à la moitié de celle de l'hypoténuse et égale au rayon.

4. Pendant que l'élève au clavier  sort  sur l'imprimante la figure qu'il collera sur son cahier , le professeur vérifie les figures des élèves.

5. Le triangle rectangle isocèle  est rapidement réalisé à l'écran et observé ainsi que le demi triangle équilatéral sur lequel nous nous attarderons une autre fois !

TR_RECT2.FIG

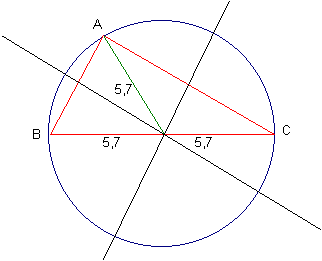
Construction d'un triangle rectangle comme ci-dessus mais aucune mesure n'est imposée.

Un autre élève est au clavier qui trace la médiatrice de chacun des côtés de l'angle droit et on vérifie que l'intersection O est le milieu de l'hypoténuse. Pouvait-on le prévoir ? On rappelle la propriété d'un point de la médiatrice d'un segment  (propriété directe et réciproque) . On retrouve le pourquoi de la construction du triangle rectangle à l'aide du cercle circonscrit.

TR_RECT3.FIG

1. Un autre élève se met au clavier. Il charge le fichier préparé, contenant trois triangles. Pour déplacer la figure à l'écran, combiner la touche  CTRL avec un glissement de la souris et pour zoomer les touches + et -

On observe un triangle a1b1c1 avec trois angles aigus et h1 son orthocentre, un triangle a2b2c2 avec un angle obtus de sommet a2 et son orthocentre h2 et un triangle rectangle ABC avec l'angle droit en A obtenu par tâtonnement, en le marquant afin de le voir devenir droit.

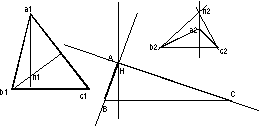
On constate que h1 est à l'intérieur du triangle a1b1c1 et que h2 est à l'extérieur du triangle a2b2c2.

2. En animant a1 et en conservant trois angles aigus h1 ne "sort" pas du triangle a1b1c1.

3. En animant a2 et en maintenant â2 obtus, h2 reste à l'extérieur du triangle a2b2c2.

4. On considère ABC. Où se trouve son orthocentre ? La réponse a du mal à venir mais certains osent et on va voir. Les hauteurs sont tracées en commençant par celles menées de B et de C. L'intersection H est bien confondue avec A. Une légère animation de A fait apparaître H tantôt à l'extérieur tantôt à l'intérieur de ABC . On trace la hauteur abaissée de A et ce sera désormais "la hauteur du triangle rectangle ABC".

On en profite pour rappeler le calcul de l'aire d'un triangle rectangle de deux façons différentes : Demi-produit de la mesure de "la" hauteur par celle de l'hypoténuse ou demi-produit des mesures des côtés de l'angle droit.