Niveau

Classe de quatrième.

Objectifs

Revoir la propriété de la droite des milieux dans le triangle , l'appliquer plusieurs fois de suite en obligeant les élèves à parler. Et revoir également les différentes propriétés des parallélogrammes.

Prérequis

L'ensemble de la classe est déjà familiarisé avec Cabri-Géomètre et en particulier l'élève qui est au clavier.
Bien sûr ne rien ignorer des leçons précédentes si possible !

Organisation pratique

Ordinateur « Tableau noir » : un PC + tablette à rétroprojeter et le logiciel Cabri-Géomètre.
Instruments de dessin pour les élèves .
La feuille photocopiée représentant les quatre quadrilatères sur lesquels on fera apparaître les constructions et les résultats importants.

Description

Durée : moins d'une heure.

Etude des différentes formes du polygone de Varignon. Le géomètre est utilisé pour présenter le problème de manière vivante et attractive.

Un fichier contenant quatre figures correspondant au cas général et aux cas particuliers a été préparé par le professeur avant le cours (fichier VARIGNON.FIG). Les différentes figures sont examinées les unes après les autres, déformées, mesurées,...

Bilan

Vive animation des élèves.

Déroulement du cours

Préparation

Un fichier contenant quatre figures correspondant au cas général et aux cas particuliers a été préparé par le professeur avant le cours (fichier VARIGNON.FIG) Les différentes figures ne sont pas visibles simultanément à l'écran. On passe de l'une à l'autre en "déplaçant l'écran sur la feuille de dessin" (touche CTRL combinée avec le glissement de la souris).

Toutes les constructions et animations qui ont eu lieu ne figurent pas ici, seulement quelques commentaires  sur chaque figure. Le logiciel n'est là que pour susciter l'intérêt et aider le professeur dans son animation de la classe.

Un parallélogramme

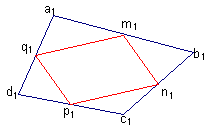
Après avoir déformé plusieurs fois la figure "PL" les élèves sont tombés d'accord qu'il fallait tracer les diagonales. Un groupe a proposé de démontrer que MNPQ est un parallélogramme en utilisant la définition, n'ayant retenu que le parallélisme des côtés avec les diagonales dans les différents triangles obtenus. Un autre groupe a trouvé plus rapide d'utiliser deux côtés opposés parallèles et de même longueur.

MNPQ est donc un parallélogramme quelle que soit la forme du quadrilatère de départ. On n'y reviendra plus !

Un rectangle

On fait apparaître la figure "RE" à l'écran  (rapidité du procédé !).

Cette fois MNPQ semble être un rectangle. Alors quand est-ce qu'un parallélogramme est un rectangle ? Il faut un angle droit ....mais où aller le chercher ? Pas évident !

Mais il ne faut pas attendre trop de temps pour qu'un élève mette bout à bout les bonnes choses maladroitement exprimées par certains et on constate donc qu'il suffit que les diagonales de ABCD soient perpendiculaires. On le note au-dessus de la figure.

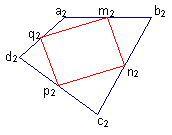
Un losange

On fait alors apparaître la figure "LO" qui par ces deux lettres oriente les recherches ! Mais alors quand donc un parallélogramme est-il un losange ?

Beaucoup ont oublié, mais on leur rafraîchit la mémoire et alors la solution arrive. Il suffit que deux côtés consécutifs soient de même mesure et par conséquent les diagonales de ABCD doivent être de même longueur : on vérifie qu'elles mesurent chacune 7 cm. On note cela sous la figure.

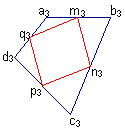
Un carré

On en arrive enfin au dernier cas "CA"...! Après avoir laissé se dire beaucoup de choses bonnes et moins bonnes on aboutit au constat que si le carré est à la fois un rectangle et un losange alors on doit avoir les diagonales de ABCD perpendiculaires et de même longueur, ce que l'on observe à l'écran et que chacun vérifie sur sa feuille en mesurant l'angle formé par les deux diagonales et en constatant que chacune d'elles mesure 6,8 cm. Un élève propose d'écrire sous la figure "Carré = Rectangle + Losange" ce qui est fait sur le champ !