Sections planes de solides

Clg Ausone, Bazas Équipe académique Mathématiques Bordeaux, octobre 2003

 

Niveau

Troisième

Objectifs

Pour les élèves de collège, la principale difficulté est d’extraire une figure plane à partir de la figure en 3D, de voir les angles droits, les segments de même longueur, etc.

Il s’agit ici de leur permettre de visualiser la nature des intersections, de dessiner en vraie grandeur ces intersections et de calculer leurs dimensions. Dans certains cas, dessiner les patrons des deux solides obtenus.

L’utilisation de Géospace et la facilité avec laquelle on peut mettre un plan quelconque de face permet de remédier à ces difficultés. Il reste à justifier (quand on dispose des outils mathématiques nécessaires).

Prérequis

Le professeur doit savoir utiliser Géospace.

Les transformations de l’espace utilisées dans ces imagiciels ne sont pas à la portée d’un élève de collège.

Organisation pratique

On fournit ici les fichiers seccyl.g3w, seccone.g3w, secprism.g3w, secsph.g3w, volupyra.g3w que le professeur utilise en classe avec un ordinateur et un vidéo projecteur.

Description

Les imagiciels proposés permettent de visualiser différentes sections de solides.

Bilan

L’utilisation de Géospace permet, sinon de démontrer, tout au moins de convaincre… L’utilisation presque systématique de ce type de logiciel change les habitudes des élèves ; la représentation d’une figure de l’espace n’est plus une figure plane comme une autre, il est possible de changer d’angle de vue. On peut dessiner une face en vraie grandeur et constater que ce qui semblait n’être qu’un parallélogramme sur la représentation 3D est en fait un rectangle ou un carré.

 

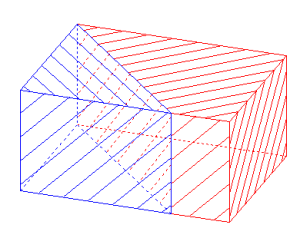
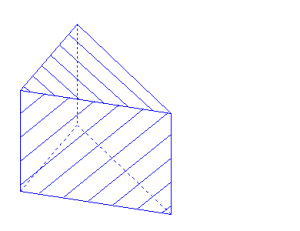
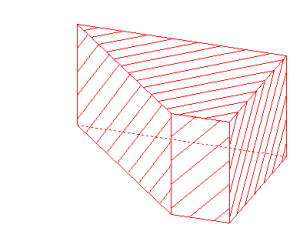
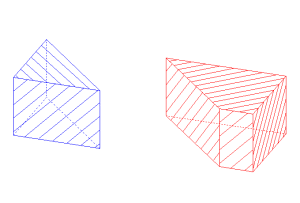
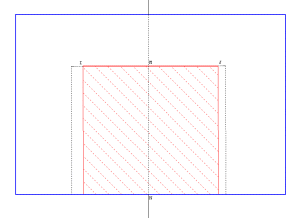
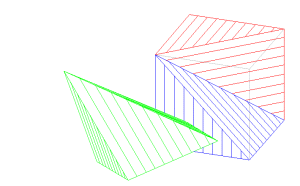
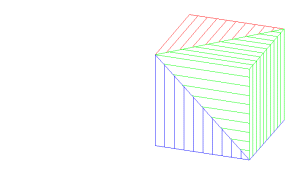
Section d’un pavé droit

Un plan mobile autour d’une arête vient couper le pavé en deux parties ; il est possible de séparer ces parties et d’en obtenir un patron.

La touche T permet de modifier à l’aide des flèches du clavier la position du plan de section
La touche 5 permet de ne visualiser que le solide bleu
La touche 4 permet de ne visualiser que le solide rouge
La touche S permet de lancer l’animation de séparation des deux solides
La touche 1 permet de développer à l’aide des flèches du clavier le solide rouge. La touche 2 permet de développer à l’aide des flèches du clavier le solide bleu.
La touche F permet de placer de face le plan de base du pavé droit ; si l’un des patrons est développé, on l’obtient ainsi en vraie grandeur.

Remarque :la combinaison de touches CTRL+F1 permet à tout moment de revenir à la vue initiale.

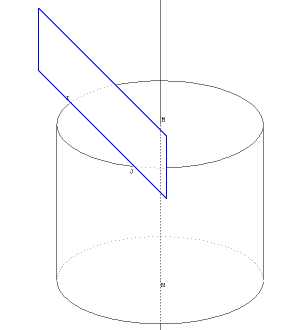
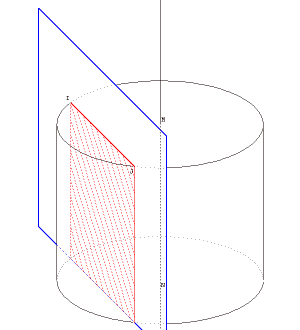
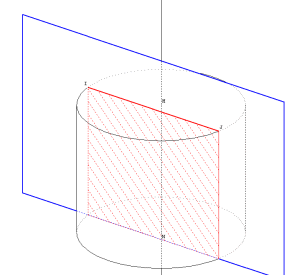
Section d’un cylindre

Un plan mobile parallèle à l’axe vient couper un cylindre ; on pourra examiner la section de face.

La touche C lance le « sectionnement automatique du cylindre » par un plan parallèle à son axe.
La touche 0 (zéro) permet de remonter complètement le « couperet ». La touche T permet de le remonter ou de le descendre pas à pas.
La touche R permet de modifier à l’aide des flèches du clavier l’orientation du plan de section.
La touche F permet de placer la section de face.

Remarque :la combinaison de touches CTRL+F1 permet à tout moment de revenir à la vue initiale.

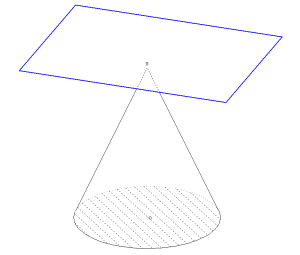
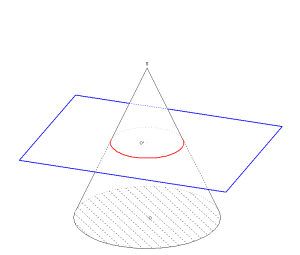
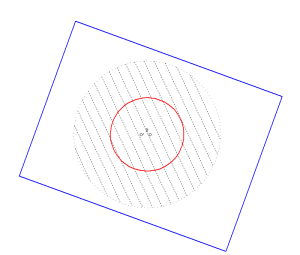
Section d’un cône

Un plan mobile perpendiculaire à l’axe vient couper le cône ; on peut examiner la section de face.

Le cône et le plan de section.
La touche T permet de déplacer à l’aide des flèches le plan de section.
La touche F permet de placer le plan de section de face.

Remarque :la combinaison de touches CTRL+F1 permet à tout moment de revenir à la vue initiale.

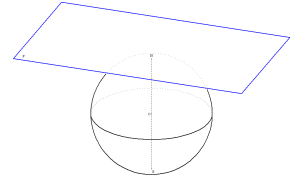
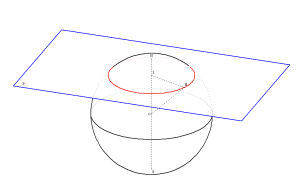
Section d’une sphère

On visualise l'intersection d'une sphère de centre O par un plan mobile P

[SN] est le diamètre de la sphère perpendiculaire à P

I est le point d'intersection de [S]) et du plan P

Le cercle rouge est l'intersection du plan P  et de la sphère

M est un point mobile sur ce cercle

Le plan P et la sphère.
La touche T permet de déplacer le plan P à l’aide des flèches du clavier afin de visualiser son intersection avec la sphère ; cette intersection est le cercle de centre I ; M est un point mobile sur ce cercle. La touche M permet de déplacer le point M à l’aide des flèches du clavier.
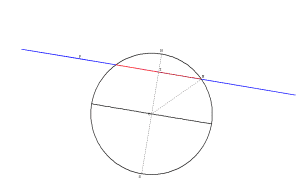
La touche R permet de placer le plan MOI de face.
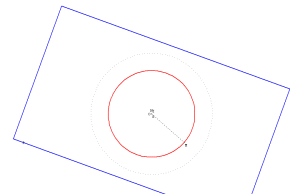
La touche F permet de placer le plan P de face.

Remarque :la combinaison de touches CTRL+F1 permet à tout moment de revenir à la vue initiale.

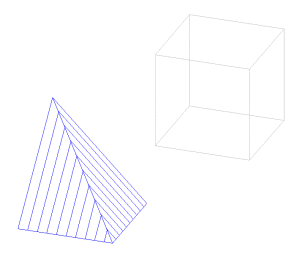
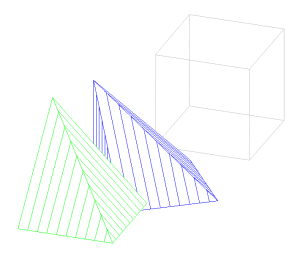
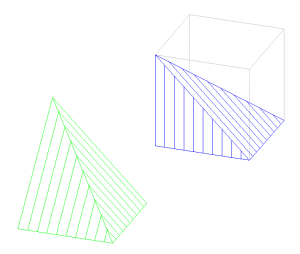
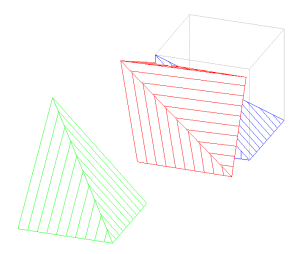
Trois pyramides pour un cube

Version informatique de la construction de 3 pyramides trirectangles, de base carré de côté c, de hauteur c, dont la juxtaposition permet de reconstituer le cube d’arête c.