| Statistiques |
| Clg La Réole (33) Groupe Math-Info, Bordeaux, juin 2001 |
Niveau
Troisième.
Objectifs
Réviser ou découvrir, de façon attractive, les différentes représentations
des séries statistiques.
Montrer la puissance, la rapidité, l’intérêt de l’outil informatique dans la
représentation des séries statistiques.
Prérequis
En principe les élèves ont déjà vu un peu de statistiques en
quatrième, mais aucun prérequis n’est nécessaire.
Pour une telle activité il est souhaitable que les élèves connaissent quelques
rudiments de fonctionnement du tableur et qu’ils aient déjà manipulé le tableur
en classe de technologie.
Organisation pratique
Compatibles PC, 2 élèves par poste, en demi groupe pour les besoins de l'expérience, logiciel works pour windows.
Cette séquence a fait l’objet de deux expérimentation. Lors de la première, la durée prévue était de deux heures en classe plus le temps nécessaire pour faire les exercices à la maison, les élèves ayant peu de connaissances sur le tableur. Cela s’est révélé nettement inssuffisant.
Pour la deuxième, les élèves ont d’abord eu une initiation au tableur en classe de technologie (deux heures). Trois heures ont été ensuite nécessaires : deux pour la leçon et une heure pour permettre aux élèves de vérifier leurs exercices avec le logiciel.
Description
Travaux dirigés sur les statistiques, en fin d'année. Toute la leçon se passe sur ordinateur.
On fournit aux élèves les séries de données (elles traduiront des situations bien connues des élèves : la classe). Ils doivent les analyser.
L'ordinateur joue ici le rôle d'un imagiciel. Il permet de faire rapidement des des dessins, modifiables instantanément.
Bilan
Le logiciel, par sa modernité, permet une approche plus attractive des statistiques. Il suscite l’intérêt des élèves qui ne sont pas lassés par la construction de graphiques différents. Ces derniers ne se lassent pas devant le grand nombre d’exercices.
L’heure complémentaire pour la correction des exercices faits à la maison est une heure d’approfondissement et de confirmation.
Il est indispensable que cette activité soit précédée par une initiation des élèves au tableur en classe de technologie.
Document élève
Première série
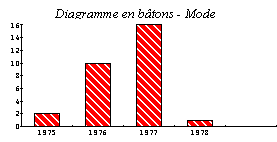
On donne le tableau suivant représentant l'année de naissance des élèves de la classe.
| année |
eff. |
| 1975 |
2 |
| 1976 |
10 |
| 1977 |
16 |
| 1978 |
1 |
1. Tracez le diagramme en bâton des effectifs. L'année correspondant au plus grand effectif s'appelle le mode de la série. Quel est-il ?
2. Entrez ces données dans le tableur et représentez le diagramme en bâton. Transformez-le en diagramme circulaire.
Sur ce dernier Works affiche les fréquences. Ajoutez ce qu'il faut dans votre feuille de calcul pour que Works calcule ces fréquences.
3. Ajoutez ce qu'il faut à votre feuille de calcul pour que Works calcule les effectifs cumulés croissants. Représentez sur un même graphique les effectifs et les effectifs cumulés croissant. Dites en deux phrases ce que représente chacun des rectangles correspondant à l'année 1977.
4. L'effectif de la classe demeurant 29 élèves, modifiez le tableau de façon que le mode soit 1976. Observez les graphiques associés.
Sachant qu'il y a au moins un individu né lors de chaque année représentée dans le tableau, quel est le plus petit effectif possible de la valeur modale ? quel est le plus grand ?
Deuxième série
| Note |
Eff. |
Note |
Eff. |
Note |
Eff. |
| 0 |
0 |
7 |
1 |
14 |
2 |
| 1 |
1 |
8 |
0 |
15 |
0 |
| 2 |
1 |
9 |
1 |
16 |
1 |
| 3 |
1 |
10 |
2 |
17 |
0 |
| 4 |
0 |
11 |
4 |
18 |
0 |
| 5 |
2 |
12 |
5 |
19 |
0 |
| 6 |
2 |
13 |
2 |
20 |
0 |
Les élèves de troisième 1 on obtenu les notes suivantes à un devoir de mathématiques.
1. Reproduisez ce tableau dans une feuille de calcul de Works. Quel est le mode ? Ajoutez une colonne permettant de calculer les effectifs cumulés.
2. Les notes étant rangées par ordre croissant, la médiane est la note à partir de laquelle la moitié des élèves au moins obtiennent un score inférieur ou égal à cette note. Pour la trouver il suffit de regarder les effectifs cumulés. Quelle est cette médiane ?
3. Faites calculer au tableur la moyenne des élèves de la classe. Énoncez une phrase (ou plus) permettant d'expliquer à un de vos camarades comment il peut calculer cette moyenne.
4. Simulation
L'effectif de la classe demeurant 25 élèves, élaborez un tableau dans chacun des cas suivants : la médiane est 12, le mode est 14, la moyenne est 11, les trois conditions précédentes sont satisfaites.
Troisième série
Six candidats ont obtenu les notes suivantes à un examen :
| Coefficients |
6 |
1 |
3 |
| Prénoms |
Maths |
H&G |
Franç |
| Marcel |
7 |
14 |
13 |
| Dorothée |
12 |
15 |
14 |
| Philippe |
17 |
5 |
7 |
| Marc |
5 |
12 |
13 |
| Marie |
19 |
14 |
15 |
| Hélène |
3 |
13 |
11 |
1. Reproduisez ce tableau dans une feuille de calcul de Works. Représentez par un diagramme en barre les notes obtenues par chaque élève dans chaque matière.
2. Si on ne tient pas compte des coefficients, il faut 30 point pour être admis. On peut dire aussi qu'un élève est reçu si le cumul de ses notes est supérieur ou égal à 30. Works possède l'option "histogramme cumulé" qui permet, pour chaque élève, de représenter ce cumul par un rectangle en mettant en évidence la part de chaque matière. Faites le dessin. Quels seraient les élèves admis ?
3. Si on tient compte des coefficients, il faut 100 points pour être reçu. Faites calculer à Works un tableau appliquant le coefficient à chacune des notes. Cela donnera par exemple pour Marcel 42, 14, 39. On veut bien sûr que toute modification du tableau initial entraîne immédiatement celle du tableau "coefficienté". Représentez les trois séries de notes à l'aide de l'option "histogramme cumulé". Quels sont les candidats reçus ?
Faites calculer à Works la moyenne de chacun.
4. Si les maths avaient eu pour coefficient 4, l'histoire 2 et le français 5, quels seraient les candidats reçus ? quelle serait la moyenne de chacun ?
NB : si votre feuille a été correctement construite, le résultat est immédiat.
Exercices à chercher à la maison
Ils seront vérifiés ultérieurement sur le tableur.
1. Représentation circulaire
On donne le tableau des effectifs du collège par niveau :
| Classes |
Effectifs |
| 3° |
134 |
| 4° |
132 |
| CPA |
14 |
| 5° |
213 |
| 6° |
180 |
| SES |
16 |
On veut représenter ces données à l'aide d'un diagramme circulaire. En utilisant votre calculatrice, dressez un tableau représentant les fréquences et les angles en degrés de chaque part du diagramme, puis faites le dessin.
Construisez aussi la représentation semi-circulaire de ces données.
2. Histogramme simple et empilé
On donne les effectifs du collège par niveau différenciés :
| Classes |
Classiques |
Adaptées |
Techno |
| 6 |
164 |
16 |
|
| 5 |
177 |
36 |
|
| 4 |
87 |
18 |
27 |
| 3 |
108 |
26 |
Représentez l'histogramme simple des effectifs par niveaux différenciés puis l'histogramme cumulé des effectifs pour chaque niveau.
3. Médiane, moyenne, mode
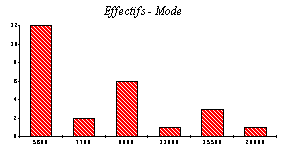
On donne le tableau suivant des salaires dans une entreprise
| Fonctions |
Salaires |
Effectifs |
| Ouvriers |
5 600 |
12 |
| Secrétaires |
7 700 |
2 |
| Techniciens |
8 800 |
6 |
| Secrétaire Direction |
11 000 |
1 |
| Ingénieurs |
15 500 |
3 |
| P.D.G. |
28 000 |
1 |
Calculez la "masse salariale", c'est-à-dire le montant total des salaires versés par l'entreprise à ses employés. En déduire le salaire moyen d'un employé. Ce salaire donne-t-il une idée exacte des salaires versés dans l'entreprise ?
À l’aide des graphiques, trouvez la médiane et le mode. Comparez le mode, la médiane et la moyenne.
Document professeur
Première série
Il s’agit d’étudier la répartition des élèves en fonction de leur année de naissance. Le tableau étant petit, les données sont vite entrées.
| année |
eff. |
| 1975 |
2 |
| 1976 |
10 |
| 1977 |
16 |
| 1978 |
1 |
Premier graphique : diagramme en bâtons des effectifs, découverte du mode.

Deuxième graphique : représentation circulaire. Découverte des fréquences (que calcule Works)
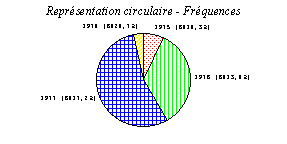
On complète la feuille de calcul, par les calculs des fréquences.
| année |
eff. |
fréquences |
| 1975 |
2 |
6,9 |
| 1976 |
10 |
34,5 |
| 1977 |
16 |
55,2 |
| 1978 |
1 |
3,4 |
| Total |
29 |
100 |
Troisième graphique : effectifs cumulés.
On ajoute une colonne pour calculer les cumuls. Un peu de réflexion est nécessaire...
| Total |
29 |
100 |
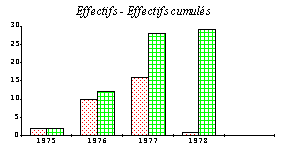
Modification du mode à effectif constant.
Ne pose pas de problème. Le graphique s’adapte automatiquement.
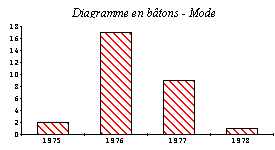
Le plus grand effectif possible pour la valeur modale est facile à trouver. Le plus petit nécessite un peu de réflexion.
Deuxième série
Il s’agit d’étudier les notes obtenues à un devoir.
1. Un exemple de calcul des effectifs cumulés a été fait à la question précédente. Le calcul ne pose plus de problème.
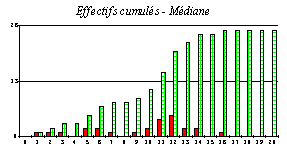
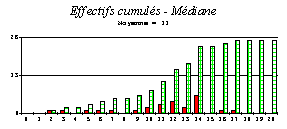
2. La notion de médiane pose quelques problèmes de compréhension. Le tableur ne permet pas de tracer le droite d’équation y = 13. On a recours à une graduation particulière : toutes les 13 unités...
3. Pour calculer la moyenne, il faut ajouter une colonne au tableau contenant, pour chaque ligne, le produit de l’effectif par la note.
| Notes |
Effectifs |
Eff cum |
Note x Eff |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 2 |
1 |
2 |
2 |
| 3 |
1 |
3 |
3 |
| 4 |
0 |
3 |
0 |
| 5 |
2 |
5 |
10 |
| 6 |
2 |
7 |
12 |
| 7 |
1 |
8 |
7 |
| 8 |
0 |
8 |
0 |
| 9 |
1 |
9 |
9 |
| 10 |
2 |
11 |
20 |
| 11 |
4 |
15 |
44 |
| 12 |
5 |
20 |
60 |
| 13 |
2 |
22 |
26 |
| 14 |
2 |
24 |
28 |
| 15 |
0 |
24 |
0 |
| 16 |
1 |
25 |
16 |
| 17 |
0 |
25 |
0 |
| 18 |
0 |
25 |
0 |
| 19 |
0 |
25 |
0 |
| 20 |
0 |
25 |
0 |
| Total |
25 |
238 |
|
| Moyenne |
9,52 |
4. Le calcul étant refait à chaque changement de valeur dans une colonne, le tableur permet de faire facilement la simulation. Beaucoup de tâtonnements sont nécessaires.
Troisième série
1. Représentation des notes obtenues par les élèves :
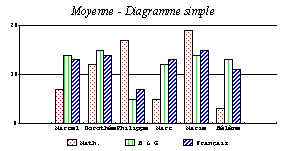
2. Pour être reçu, il faut que la somme des notes soit supérieure ou égale à 30. La notion d’histogramme cumulé prend ici tout son sens. Le dessin « parle ».
On fait apparaître la droite d’équation y = 30 en graduant l’axe des ordonnées toutes les 30 unités...
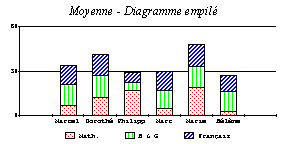
3. Calcul des moyennes en tenant compte des coefficients.
L’admissibilité est à 100.
La simulation devient un jeu : comment jouer sur les coefficients pour que faire pour que Philippe soit reçu ? Pour que Marcel soit collé ? ...
Exercices à faire à la maison
A chercher à la « main ». Ils seront vérifiés ultérieurement sur le tableur.
1. Représentation circulaire
Effectifs du collège par niveau.
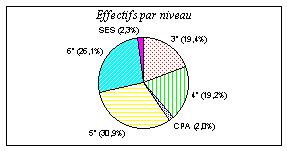
Calcul des fréquences.
Construire aussi la représentation semi-circulaire.
2. Histogramme simple et empilé
Niveaux différenciés (classique, adapté, technologique).
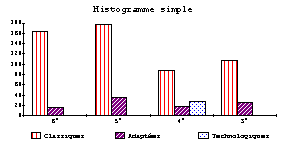
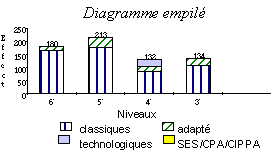
3. Médiane, moyenne, mode
Salaires dans une entreprise.
Exploitation de ces trois notions.