Articuler l'aide en maths et l'aide en français : exemples |
|
Réunion du 2 octobre 2002 |
|
Faire le bon choix des mots de liaison
(D’après : Mathématiques en seconde - CRDP de LILLE)
Compléter les phrases par l’un des mots suivants : si, alors, donc, comme, lorsque
— ...... deux droites sont perpendiculaires à une même droite,.........elles sont parallèles.
— ABCD est un parallélogramme, ......... ses diagonales se coupent en leur milieu.
— ...... I est le milieu de [AB], on a AI = IB.
— ...... un parallélogramme a deux côtés consécutifs de même longueur,...... c’est un losange.
— Le triangle ABC est inscrit dans un cercle de diamètre [BC], ....... il est rectangle en A.
— ......... deux droites sont parallèles à une même droite, elles sont parallèles.
— ......... le triangle ABC a ses côtés [AB] et [BC] de même longueur, il est isocèle en B.
— ......... un point M appartient à la médiatrice d’un segment, il est équidistant des extrémités de ce segment.
— Les droites D et D’ du plan P sont perpendiculaires à une même droite de ce plan, ......... elles sont parallèles.
— ......... un quadrilatère ABCD a ses diagonales [AC] et [DB] qui se coupent perpendiculairement en leur milieu, ......... c’est un losange.
— .........les droites D et D’ sont coplanaires et non parallèles, elles sont sécantes.
Écrire un texte argumentatif
Gérer les articulations logiques
(d’après le cahier 1 d’aide à l’évaluation en Français - DE&P)
Item 1
Restituer à ces phrases leurs articulations logiques pour que le texte soit cohérent.
......... les jeunes aiment à s’exprimer sans contraintes, ils sont heureux d’avoir la parole sur les ondes. Les radios libres, ....... elles donnent l’impression (ou l’illusion ?)de les écouter, semblent répondre à ce vœu. ......... certains dérapages récents laissent à penser qu’il est plus malaisé qu’il n’y paraît de jouer la carte de la liberté absolue du direct. ........ ... n’y a-t-il pas de la démagogie dans le choix de sujets plus ou moins choquants, sous prétexte d’ouvrir l’antenne aux problèmes intimes des adolescents ?
Item 2
Rédiger, en quelques phrases, un message publicitaire en faveur du tourisme vert. Organiser les arguments ci-dessous à l’aide des liens logiques choisis dans la liste jointe, en n’omettant pas les transformations rendues éventuellement nécessaires sur les formes verbales.
Arguments :
— l’air pur et l’espace sont bénéfiques pour la santé du citadin surmené.
— l’image de la campagne tend à se modifier.
— un village isolé offre apparemment peu d’intérêt.
— vous reviendrez sans aucun doute jouir de ces doux paysages ;
— seuls les amoureux de la nature méritent de la découvrir.
— de nombreuses activités vous seront proposées pour des vacances dynamiques.
Liens logiques :
bien que, pourtant, mais, malgré, ainsi que, néanmoins, c’est pourquoi, cependant, en conséquence, aussi, certes, car, d’ailleurs.
Démonstration puzzle
(D’après : Mathématiques en seconde-CRDP de LILLE)
Texte
ABC est un triangle rectangle en A.
H est le pied de la hauteur issue de A dans le triangle ABC.
I et J sont les milieux respectifs de [BH] et [AH].
Démontrer que les droites (AI) et (CJ) sont perpendiculaires.
Démonstration à reconstituer
— donc les droites (AI) et (CJ) sont perpendiculaires.
— donc la droite (IJ) est la hauteur issue de I dans le triangle ACI.
— par hypothèse, ABC est un triangle rectangle en A, donc les droites (AB) et (AC) sont perpendiculaires..
— donc la droite (IJ) eest perpendiculaire à la droite (AC).
— par hypothèse, dans le triangle ABH, on a I milieu de [BH] et J milieu de [AH].
— de plus la droite (AH) est la hauteur issue de A dans ke triangle ACI.
— si deux droites sont parallèles, toute perpendiculaire à l’une est perpendiculaire à l’autre.
— donc les droites (IJ) et (AB) sont parallèles.
— donc J, point d’intersection des droites (AH) et (IJ) est....
— par conséquent, la droite (CJ) est la hauteur issue de C dans le triangle ACI
— l’orthocentre du triangle ACI.
Raisonnement à plusieurs arguments
(D’après : Mathématiques en seconde-CRDP de LILLE)
Énoncé
ABC est un triangle non rectangle, O est le centre du cercle circonscrit au triangle ABC, H est l’orthocentre du triangle ABC, M est le milieu de [BC], A’ le symétrique de A par rapport à O.
Démontrer que M est le milieu du segment [A’H]
Travail à effectuer
1. Corriger les quatre solutions incorrectes proposées :
— en notant dans la marge l’une des annotations suivantes :
déduction fausse - déduction vraie mais non justifiée - déduction vraie mais insuffisamment justifiée - déduction vraie mais inutile - affirmation fausse - affirmation vraie mais non justifiée - affirmation vraie mais insuffisamment justifiée,
ou toute autre annotation pertinente.
— en entourant dans le texte le « donc » exprimant les déductions annotées. Pour les déductions fausses, fournir un contre-exemple.
— en soulignant dans le texte chaque affirmation à corriger.
2. Rédiger ensuite une solution correcte.
Première solution incorrecte
Dans le triangle ABC, (AH) est la hauteur issue de A, donc les droites (AH) et (BC) sont perpendiculaires.
La droite (OM) est la médiatrice de [BC], donc la droite (OM) est perpendiculaire à la droite (BC).
Par suite, les droites (OM) et (AH), perpendiculaires à la même troisième (BC), sont parallèles.
Ainsi dans le triangle AHA’, la droite (OM) passant par le milieu O de [AA’] et parallèle à la droite (AH) coupe [HA’] en son milieu.
Donc M est le milieu de [A’H.]
Deuxième solution incorrecte
Par hypothèse, H est l’orthocentre du triangle ABC. Donc 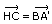 .
.
Donc HCBA’ est un parallélogramme.
Donc  et
[HA’] et [BC] se coupent en leur milieu.
et
[HA’] et [BC] se coupent en leur milieu.
Or, on sait par hypothèse que M est le milieu de [BC]. Donc M est le milieu de [HA’].
Troisième solution incorrecte
On sait par hypothèse que M est le milieu de [BC], donc  .
.
Donc 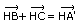 .
.
Donc HBA’C est un parallélogramme.
Or, on sait que M est le milieu de [BC], donc M est le milieu de [HA’].
Quatrième solution incorrecte
On sait par hypothèse que A appartient au cercle circonscrit au triangle ABC et que A’ est le symétrique de A par rapport à O, centre de ce cercle. Donc [AA’] est un diamètre du cercle.
De plus, C est un point du cercle distinct de A et A’, donc les droites (AC) et (A’C) sont perpendiculaires.
En outre, H est l’orthocentre du triangle ABC, donc la droite (BH) est perpendiculaire à la droite (AC).
Par suite, les droites (BH) et (A’C), perpendiculaires à la même troisième (AC), sont parallèles.
Donc BHCA’ est parallélogramme.
Or, on sait que M est le milieu de la diagonale [BC], donc M est le milieu de l’autre diagonale [HA’]