1.

Il existe un très ancien document babylonien donnant une approximation de   la racine de 2 sous la forme 1 24 51 10, en sexagésimal, c’est-à-dire, en décimal : 1, 414 212 963, au lieu de 1, 414 213 562. Pas si mal ! On trouvera une image, avec des commentaires en anglais, à l'adresse suivante, sur la Toile : http://it.stlawu.edu/~dmelvill/mesomath/tablets/YBC7289.html

Les historiens des mathématiques se sont interrogés pour savoir comment les Babyloniens avaient obtenu cette excellente approximation. Voici une réponse possible.

Elle part du problème suivant :

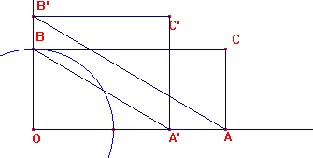
2. À partir d’un rectangle, construction d’un rectangle de même aire mais « plus trapu ». On prend une des dimensions du deuxième rectangle égal à la demi-somme des dimensions du premier.

Justifier la construction suivante : (Cabri) (A' est construit comme le milieu de deux points).

On itère, et on obtient la figure ci-contre :

On a déjà presque un carré. La troisième étape ne se distingue guère de la seconde.

Soient a_n et  b_n  les côtés du n-ième rectangle, en commençant par l’indice 0, on a les relations de récurrence :   a_n+1 = 1/2 (a_n + b_n) , et : b_n+1 = A / a_n+1 , A étant l’aire du premier rectangle.

3. Convergence : Observation

On voit bien, géométriquement, que la figure tend vers un carré. On peut donc supposer que son côté tend vers la racine carrée de A.

Or les côtés sont exprimés de proche en proche, à partir de a₀ et  b₀  par de simples additions et divisions. On peut donc obtenir par le calcul des approximations rationnelles de la racine de A aussi proche qu’on le désire.

On suppose que c’est ce qu’on fait les Babyloniens.

A ma connaissance, on ne trouve cependant pas un exposé de cette méthode dans les tablettes babyloniennes. On le trouve, beuacoup plus tard, chez Héron d’Alexandrie.

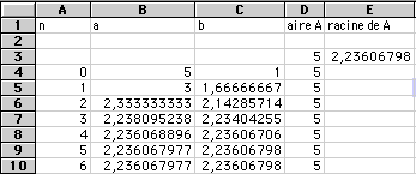
On peut calculer les premiers termes à la main,  ou les programmer sur les calculatrices, ou, comme ici, sur tableur.(Avec A=5)

5. Étude de ces suites

On a pu observer graphiquement et numériquement, que si on a au départ, comme sur notre exemple :  b_n < a_n, avec  a_{n .}b_n = A, d’où aussi  :  b_n < R <  a_n,  avec R²=A, on a aussi :

 R <  a_n+1 (à démontrer) d’où aussi :      b_n  < b_n+1 < R  <  a_n+1 <  a_n.

Mais alors :  0 <  a_n+1 - R <  a_n+1 -  b_n  = 1/2 ( a_n - b_n).

Ceci démontre alors la convergence de a_n vers R, et donne une idée de la vitesse de convergence, plus rapide qu’une suite géométrique de raison 1/2. Mais en fait, cette vitesse est encore plus rapide. (On pourrait le démontrer au paragraphe suivant). 

4.  Étude graphique classique

Si on ne considère que le grand côté du rectangle, on a la relation : a_n+1 = 1/2 (a_n + A/ a_n )_.

On a donc :  a_n+1  = f(a_n), avec f(x) = 1/2 (x + 1/x).

On peut alors représenter classiquement la suite (a_n), grâce à la représentation graphique de f.

6. Où l’on retrouve la méthode de Newton

On peut voir l’algorithme de Babylone sous l’angle suivant :

Il s’agit de résoudre l’équation x²= A, ou encore x² - A = 0. Essayons à ce propos la méthode de Newton.

Le faire à propos de la fonction g telle que  g(x) = x² - 5.

Démontrer que l’on retrouve alors l’algorithme de Babylone.