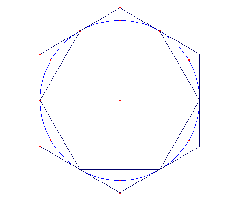
Les suites d'Archimède convergeant vers π |
|
Journée de Formation des stagiaires en situation, 2000-2001 |
|
D'après une suggestion du projet de programme de Terminale S.
|
Archimède encadre le périmètre du cercle (choisi ici avec un rayon de 1/2), par les périmètres de deux polygones réguliers. (Ici des hexagones).
Puis il double le nombre de côtés, un certains nombres de fois successivement, jusqu'à obtenir un polygone à :
6x2x2x2x2= 96 côtés.
|
Posons : c = MM' ; c' = M'M" (comme corde ou côté) ; b = OB ; b' = OB' (comme bras).
C = NN'.
On peut démontrer alors, grāce à des triangles semblables, les relations :
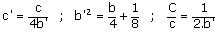 .
.
Soient les suites correspondant à un doublement du nombre de côtés à chaque fois, et notons pn et Pn les périmètres des polygones intérieurs et extérieurs à chaque étape. Les relations précédentes entraînent les suivantes :
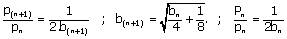 .
.
Ces relations permettent de trouver de proche en proche les termes des différentes suites suites bn , pn et Pn .
Il ne reste qu'à programmer, avec Excel :
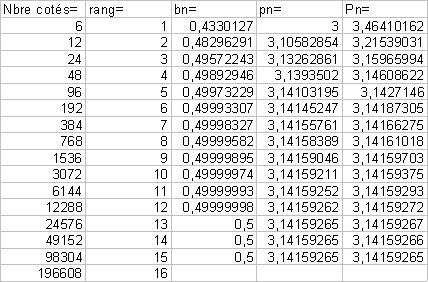
Archimède a fait à la main les calculs pour un nombre de côté égal à 96.