
Somme des inverses de distances |
|
Journée de Formation des stagiaires en situation, 2000-2001 |
|

On s'intéresse au problème suivant :
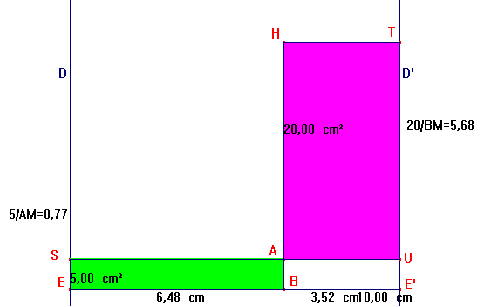
Un point B de déplace sur un segment [EE'] de côté 10 cm. On trace le rectangle BASE de côté [EB] et d'aire 5 cm2, comme sur la figure, puis le rectangle HAUT, de sommet A et comme sur la figure, mais d'aire cette fois 20 cm2.
Cela peut se faire sous CABRI, comme ici, sans trop de difficulté. On peut
le faire aussi à la main.
Sous CABRI, on peut faire bouger le point B :
QUESTION
:
On s'intéresse
aux variations de la longueur BH. Pour quelle position de B, BH est-elle minimale
?
On peut utiliser le mode "Trace" ou "Lieu" de CABRI :
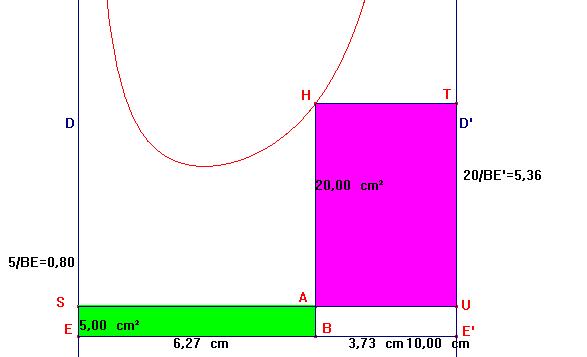
Ca donne déjà une idée.
Il reste à formaliser, de façon littérale,
à explorer avec la calculatrice graphique,
à conjecturer,
à démontrer.
SOLUTION
On pose EB=x et BH=f(x). Alors f(x)=5/x + 20/(10-x).
On programme (Excel) : Voir ci-dessous
|
X |
f(X) |
X |
f(X) |
|
|
0 |
3,25 |
4,5014245 |
||
|
1 |
7,22222222 |
3,26 |
4,50110138 |
|
|
2 |
5 |
3,27 |
4,50082019 |
|
|
3 |
4,52380952 |
3,28 |
4,50058072 |
|
|
4 |
4,58333333 |
3,29 |
4,50038277 |
|
|
5 |
5 |
3,3 |
4,50022614 |
|
|
6 |
5,83333333 |
3,31 |
4,50011064 |
|
|
7 |
7,38095238 |
3,32 |
4,50003607 |
|
|
8 |
10,625 |
3,33 |
4,50000225 |
|
|
9 |
20,5555556 |
3,34 |
4,50000899 |
|
|
10 |
#DIV/0! |
3,35 |
4,50005611 |
|
|
3,36 |
4,50014343 |
|||
|
3,37 |
4,50027078 |
|||
|
3,38 |
4,50043798 |
|||
|
3,39 |
4,50064486 |
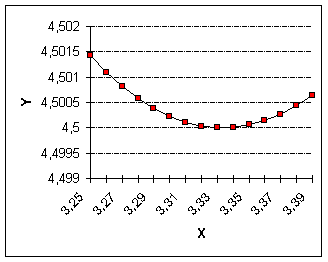
On se rend compte qu'il semble que f admette un minimum valant 9/2, atteint pour x = 10/3.
Or il est aisé de démontrer que f(10/3) = 9/2.
On peut même démontrer qu'il y a effectivement minimum, en mettant 5/x + 20/(10-x) - 9/2 au même dénominateur. En factorisant, trouve en effet, après calcul : (3x-10)^2 / (x(10-x)).