Joints d’étanchéité

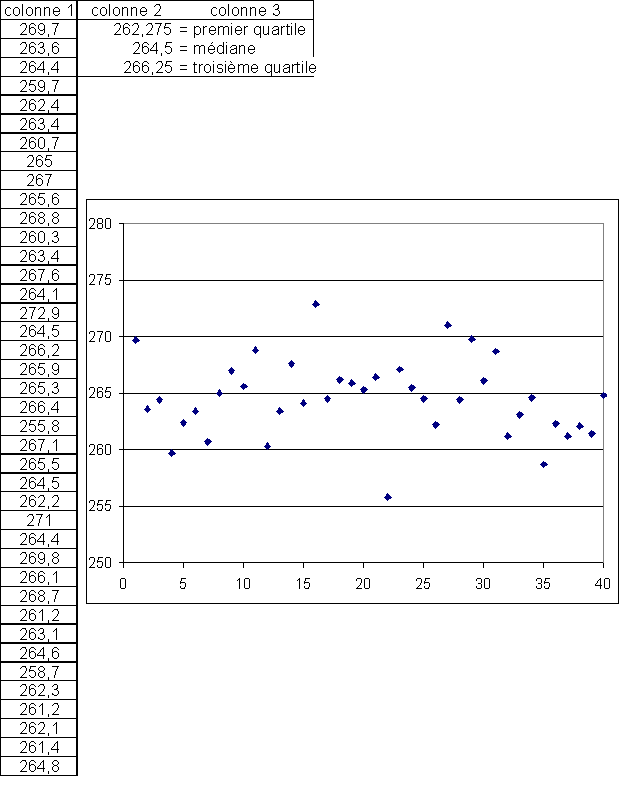
Une machine déverse du caoutchouc de façon continue dans un moule pour fabriquer des joints d’étanchéité que l’on utilise dans l’industrie automobile. On veut contrôler la régularité de l’écoulement du caoutchouc dont les variations affectent les dimensions du joint. On effectue alors des mesures sur cette machine pendant une demi-heure et on obtient des masses de caoutchouc en grammes, chacune étant obtenue par un écoulement de caoutchouc d’une durée de 30 secondes.

Les 40 mesures ainsi obtenues ont été analysées par un tableur, dont les résultats figurent à la page 2 :

• la colonne 1 de la feuille de calcul contient les 40 mesures en grammes,
• les colonnes 2 et 3 contiennent le premier quartile, la médiane et le troisième quartile.
• Le graphique représente les 40 valeurs obtenues chronologiquement.

1) Construire un diagramme en boîte (appelé aussi boîte à moustache ou boîte à pattes) permettant une première analyse des valeurs du contrôle.

2) Quel pourcentage des valeurs obtenues lors de ce contrôle se trouvent entre 261,2 et 267,6 ?

3) On peut considérer comme aberrantes des valeurs qui sont supérieures à Q₃ + 1,5 I ou inférieures à Q₁ - 1,5 I, où I désigne l’intervalle interquartile, Q₁ le premier quartile et Q₃ le troisième quartile. Le contrôle sur la machine fait-il apparaître des valeurs aberrantes ? Lesquelles ? 

4) Deux autres machines du même type ont été contrôlées de manière plus approfondie. Pour chacune d’elles 1126 mesures ont été effectuées. Elles ont été analysées à l’aide d’une calculatrice, qui a donné les deux diagrammes en boîtes qui figurent ci-dessous :

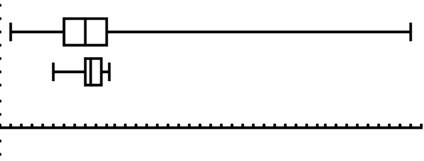
Le diagramme qui figure en haut de l’écran de la calculatrice représente les mesures effectuées sur la machine 1. La médiane obtenue est de 265,8, le premier quartile est de 265,4, le troisième quartile est de 266,2.

Le diagramme qui figure en-dessous représente les mesures effectuées sur la machine 2. La médiane obtenue est de 265,9, le premier quartile est de 265,8, le troisième quartile est de 266,1.

Quels commentaires pouvez-vous faire de ces résultats ?