Télécharger ce document (RTF) et les fichiers Lotus et Excel associés (ZIP ; 102 Ko)

Programme

Variance, écart type
Introduction de l'écart type pour des données gaussiennes.
Définition de la plage de normalité pour un niveau de confiance donné.

Document d'accompagnement

[...] Pour l’interprétation lorsque le niveau de confiance est 0,95, on notera que le choix de ce dernier résulte d’un consensus pour avoir des formules simples et implique qu’environ une personne sur vingt sorte de cette plage.

Nous proposons ici un programme de simulation d'un échantillon d'une population suivant une loi normale. Il ne s'agit évidemment pas que les élèves comprennent la construction de la simulation ; ils constateront seulement la validité des plages de normalité.

Voir les fichiers simuloinorm.xls pour Excel et simuloinorm.123 pour Lotus

Nous donnons ci-dessous, pour les enseignants, la justification théorique du processus de simulation employé.

Théorème de la limite centrale

Si on suppose que les variables aléatoires indépendantes X_n suivent une même loi (inconnue) de moyenne m et d’écart type s, on peut dire que, pour n suffisamment grand, la variable aléatoire

Beaucoup d’auteurs indiquent que « n assez grand » veut dire n ³ 30. C’est jugé « trop rigide » par F. Dress (Probabilité - Statistique chez Dunod). Il précise qu’« on découvre vite que l’approximation normale est d’autant meilleure que la distribution initiale est continue (c’est la condition primordiale), régulière et symétrique (le pire étant donc la loi de Bernoulli de paramètre p petit ou voisin de 1). Pour les meilleurs cas, n ³ 10 voire moins est une suggestion raisonnable, pour les mauvais, n ³ 30 peut ne pas être suffisant… »

Application

Dans toute calculatrice ou tout tableur, il existe une fonction qui simule le tirage au hasard d’un nombre entre 0 et 1 ; sur Excel, il s’agit de la fonction ALEA().

On suppose que cette fonction suit une loi uniforme dont la densité de probabilité est la fonction caractéristique : C_[0;1].

.

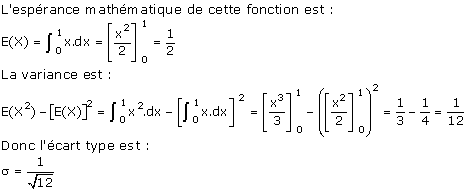En supposant que 12 est « suffisamment grand » (ce qu’on pourra vérifier plus tard par l’expérimentation), considérons la variable aléatoire :

D’après le théorème de la limite centrale, cette variable aléatoire suit approximativement une loi normale de moyenne 

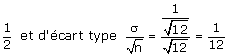
Donc la variable aléatoire 12.Y suit approximativement une loi normale de moyenne 6 et d’écart type 1 et la variable aléatoire Z = (12.Y – 6) suit approximativement la loi normale centrée réduite .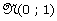

Pour simuler sur Excel une série de nombres répartis selon la loi normale centrée réduite, on entrera dans une cellule la formule :
= ALEA()+ALEA()+ALEA()+ALEA()+ALEA()+ALEA()+ALEA()+ALEA()+ALEA()+ALEA()+ ALEA()+ALEA() – 6
et on recopiera cette formule 100, 200 ou 500 fois.

Pour simuler une série de nombres répartis selon la loi normale de moyenne m et d’écart type s, on entrera dans une cellule la formule :
= s(ALEA() + ALEA() + ALEA() + ALEA() + ALEA() + ALEA() + ALEA() + ALEA() + ALEA() + ALEA() + ALEA() + ALEA() – 6) + m que l’on recopiera autant de fois que l’on voudra.

Prolongements

Si on craint que 12 soit un nombre trop petit et qu’on prenne n sommes de ALEA(), il faut un peu modifier les calculs.

On prend la variable aléatoire :

Exemple

Enfin, tout ceci reste valable pour les calculatrices en utilisant la fonction Rnd# ou Rand() à la place d’ALEA().