Objectif : Donner aux collègues les moyens de présenter simplement des familles de sujets (dans le cadre d’un thème donné), permettant ainsi aux élèves de choisir un sujet précis de TPE.
Contenu |
Exemple |
| Dans le cadre du thème " périodes ", on s’intéresse à la famille de sujets intitulée "pavages périodiques" | |
| Présentation de ce que recouvre le titre de la famille avec des illustrations directement accessibles aux élèves | Présentation de quelques exemples de pavages (dans des livres ou sur ordinateur) |
| Prérequis et connaissances mises en jeu | Isométries du plan (translations, réflexions, rotations) ; invariance d’une partie du plan par une isométrie ; composées d’isométries |
| Bibliographie de base
Sites Internet de référence |
" Le monde des pavages " de Deledicq et Raba aux
éditions du Kangourou " Totally Tessellated " " ScienceU, the Geometry Center " Logiciels " Pavages " http://wwwlogieduc.com |
| Pistes d’étude et propositions de sujets précis de TPE | Analyse de représentations de pavages que l’élève
aura trouvées Réalisation de pavages originaux soit à la main, soit sur ordinateur à l’aide de logiciels de construction Présentation de résultats mathématiques concernant les pavages ou les frises Recherche des différents polygones réguliers qui peuvent paver le plan Étude de liens avec la structure des cristaux |
Nous recommandons particulièrement le logiciel d'un collègue de l'Académie,
appelé Pavages, qui est vendu par la société logieduc à l'adresse suivante :
http://www.logieduc.com
Sur ce site est proposé une version de démonstration gratuite, permettant de construire
les pavages, mais pas de les enregistrer, ni de les imprimer. Le logiciel fonctionne sous
Windows.

On peut trouver ce pavage d’Escher, sur le site de " Totally Tesselated ".
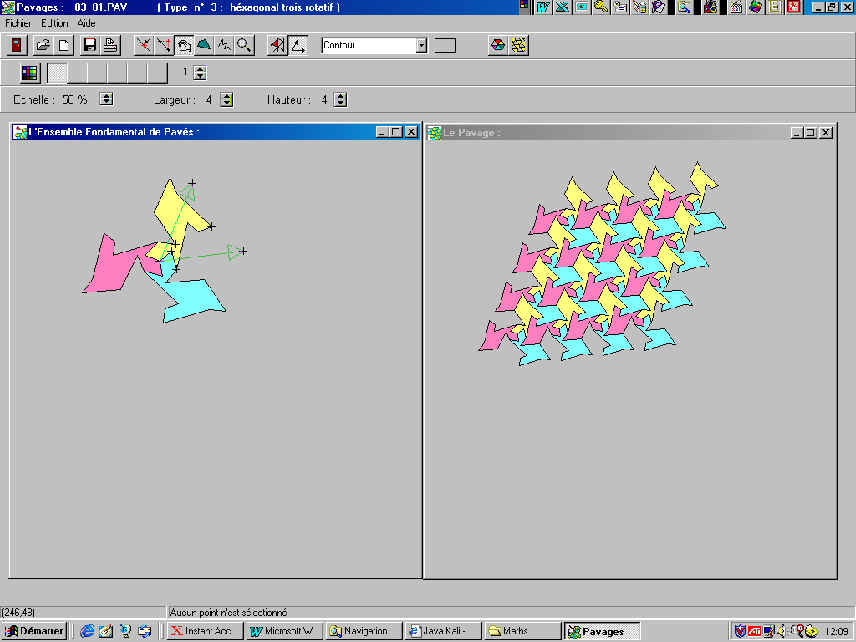
Il s’agit d’un pavage de type p6.

Un des travaux possibles d’élèves est l’analyse de ce pavage.
Les éléments géométriques qui le caractérisent sont : translations minimales, centres de rotations d’ordre 6, centres des rotations d’ordre 3.
Cette configuration caractérise un pavage de type p6.
Les élèves peuvent présenter la composition de deux des transformations mises ici en évidence.
Par exemple la composée de la rotation de centre S' et d'angle +60° et de la rotation de centre S et d'angle –60° ou la composée de la rotation de centre T et d'angle +120° et de la rotation de centre S et d'angle +60°.
On peut aller plus ou moins loin dans cet abord du concept de groupe.
On trouve les méthodes de construction de pavages dans divers ouvrages ou sur divers sites Internet (que les professeurs auront pu télécharger), souvent en anglais. Les professeurs peuvent aussi fournir une fiche-méthode à ce sujet.
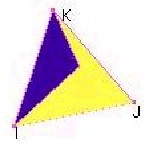
Les figures sont réalisées avec le logiciel CABRI, ou avec un autre logiciel de géométrie.
On part d'un triangle équilatéral, dans lequel on dessine le motif minimal du pavage, qui est ici bicolore.
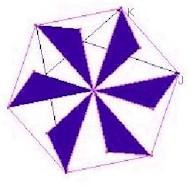
Par des rotations autour de I, on répète le motif minimal. On décore ainsi un hexagone.
Le dessin obtenu est un ensemble translaté pour le pavage.
On translate de nombreuses fois cet ensemble translaté suivant les vecteurs de translations indiqués (autrement dit, on pave le plan avec le polygone de base).
Cela donne le pavage :
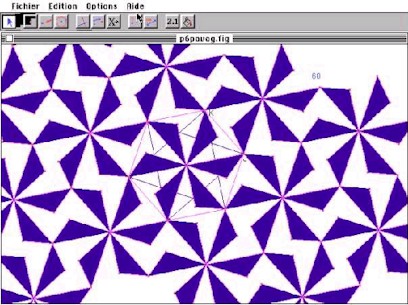
Un lien peut être fait entre pavages et cristallographie.
Les cristaux sont classés suivant l’ensemble des isométries de l’espace qui les laissent invariants. Cependant, si on coupe le cristal suivant un des plans où sont disposés les atomes, on obtient une configuration plane, et donc un pavage.
Voici ci-dessous l’exemple du graphite, donné par un professeur de l’Université du Mans, à l’adresse suivante :
http://www.univ-lemans.fr/enseignements/chimie/01/licence/cristallochimie/lecture_1/
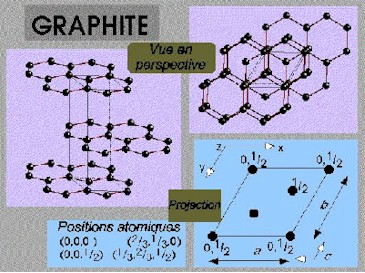
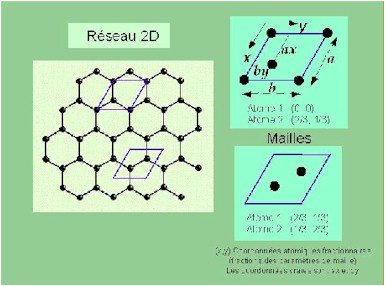
Il faut souligner cependant que si l’on se place dans un plan de coupe, où les atomes sont disposés en cellules hexagonales, le groupe de transformations n’est pas tout à fait celui rencontré précédemment ; en effet, un pavage par hexagones admet des axes de symétrie ce qui n’était pas le cas des pavages précédents. Le groupe associé à un pavage du plan par hexagones réguliers inscriptibles, réalisé par exemple par une seule couche d’atomes dans le graphite, est p6m ; celui associé aux pavages précédents était p6.
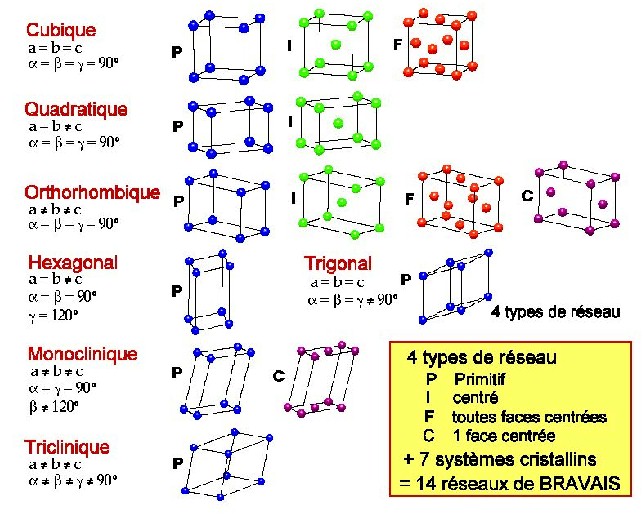
Il nous semble, mais cela demanderait à être vérifié, que le graphite rentre dans la catégorie " hexagonal " de la classification des cristaux due à Bravais.
Cette prise de contact doit se faire de façon graphique, pour le plaisir des
yeux. On pourra trouver de beaux pavages, d'Escher ou autre, dans la bibliographie
citée, mais aussi dans: http://library.advanced.org/16661/escher/tessellations.2.html
C'est une partie d'un site très complet sur les pavages, qui se nomme Totally Tesselated.
Pour une première approche, se restreindre à parcourir cette page et les suivantes,
présentant de belles images d'Escher. Les méthodes d'analyse et de construction des
pavages commencent à être abordées.
http://gainsbourg.hrsk.edu.fi/~somaires/pavages/pavages.html
Également une introduction aux pavages par l'œuvre d'Escher. La créatrice du site
habite manifestement en Finlande.
Une autre façon d'aborder les pavages est de faire tourner des logiciels spécifiques
sur les pavages.
Nous recommandons particulièrement le logiciel d'un collègue de l'Académie,
appelé Pavages, qui est vendu par la société logieduc à l'adresse suivante :
http://www.logieduc.com
Sur ce site est proposé une version de démonstration gratuite, permettant de construire
les pavages, mais pas de les enregistrer, ni de les imprimer. Le logiciel fonctionne sous
Windows.
http://www.geom.umn.edu/java/Kali/ est l'adresse d'un logiciel fonctionnant sous Java, sur PC, que l'on peut télécharger gratuitement. Ce logiciel est moins fouillé que le précédent, mais permet de réaliser des motifs fort agréables, toujours à partir du groupe des isométries du pavage.
Ci-dessous l'adresse de téléchargement, à l'Université de Dresde, en Allemagne,
d'un logiciel fonctionnant sous DOS, et exclusivement avec des ordinateurs pas trop
rapides.
http://www.math.tu-dresden.de/~ganter/ornament.html
Ce logiciel est fort agréable, malgré son côté un peu ancien, et contient également
une procédure de reconnaissance du groupe d'isométrie d'un pavage donné.
Les deux sites donnés ci-dessous sont à la fois très complets et sont très accessibles. Ils ont pour nous le seul inconvénient d'être en anglais...mais ce n'est pas insurmontable, surtout quand il s'agit de mathématiques et de géométrie.
Pour nous permettre de nous orienter, sachons que Pavage se traduit en anglais par
Tesselation ou encore Tiling, ce dernier mot provenant de Tile qui veut dire Tuile.
Un pavage doublement périodique est dénommé par un mathématicien anglophone Pavage
papier-peint, ou plus exactement wallpaper tiling.
http://library.advanced.org/16661/index2.html
Il s'agit du site Totally Tesselated. Il est consacré presque exclusivement aux pavages
doublement périodiques, et plus particulièrement aux pavages par des polygones. Les
liens qui font table des matières se trouvent dans l'image du haut. On pourra consulter
en particulier : "Essentials", "Escher".
http://www.ScienceU.com/geometry/articles/tiling/wallpaper.html
C'est la partie du site ScienceU consacrée aux pavages doublement périodiques.
Contrairement au site précédent, ces pages traitent également d'autres sortes de
pavages.
Ces deux sites peuvent être complétés par un site d'un niveau moins accessible, mais avec beaucoup de choses intéressantes...et de belles images. Voici les pages sur les pavages plans, mais Monsieur Joyce s'intéresse à de très nombreux thèmes mathématiques. http://aleph0.clarku.edu/~djoyce/wallpaper/seventeen.html
D'autres sites intéressants également, mais d'accés moins facile. De plus les pavages ou les frises ne représentent qu'une partie des sujets qu'ils traitent. On peut y trouver des informations utiles, mais il faut trier l'information, et ne pas s'y perdre.
http://bib3.ulb.ac.be/coursmath/escher.htm
Le site de ce professeur belge est impressionnant, (et en français !), mais seule
une partie est consacrée aux pavages qui nous intéressent ici.
Cette première page traite des pavages "à la Escher" (doublement
périodiques).
Une seconde adresse aboutit à de beaux pavages du plan par des polygones réguliers.
http://bib3.ulb.ac.be/coursmath/pavages.htm
Pour obtenir ces pavages, cliquer sur les différents points, sur les côtés des
triangles, qui sont associés à des triplets de rationnels.
Voici un site extrêmement complet sur les pavages ; mais, probablement, seul les
premières pages seront exploitables :
http://comp.uark.edu/%7Ecgstraus/symmetry.unit/index.html/
http://gbms01.uwgb.edu/~dutchs/symmetry/2dspcgrp.htm
Site de Monsieur Steve Dutch, de l'Université du Wisconsin. Le lien ci-dessus traite des
pavages du plan. Il y a peu d'images. Le lien ci-dessous concerne les frises.
http://http://gbms01.uwgb.edu/~dutchs/symmetry/1dspcgrp.htm
Monsieur Dutch est cristallographe. On trouvera l'index de ses pages sur les
symétries, les pavages et la cristallographie, à l'adresse suivante : http://gbms01.uwgb.edu/~dutchs/symmetry/symmetry.htm
Sur les cristaux, outre le site ci-dessus, on pourra consulter l'édition Internet
par un professeur de l'Université du Mans d'un ouvrage en anglais . http://www.univ-lemans.fr/enseignements/chimie/01/licence/cristallochimie/lecture_1/lec1.html
© S.J.Heyes, Oxford, 1996 Traduction - Adaptation : C. Jacoboni, Le Mans, 1998
Voici un texte en anglais, de niveau assez élevé, mais qui a l'avantage de donner un
exemple d'un vrai article scientifique, présenté à un congrès.
Il traite de plusieurs sujets. * Les pavages doublement périodiques semi-réguliers,
avec des polygones de plusieurs formes * Les pavages historiques de Dürer et
de Kepler. * Les pavages non périodiques * Les cristaux et les quasicristaux.
http://www.sb.fsu.edu/~caspar/201/
Parmi les liens fournis sur ces pages, il est sans doute ardu de faire un tri, et seul a priori les enseignants pourront les exploiter. Mais il y a sans doute des trésors à y découvrir.
Tout d'abord, les signets de "Totally Tesselated", fort riches : http://library.advanced.org/16661/links.html
http://www.best.com/~xah/Wallpaper_dir/c6_RelatedWebSites.html
Des liens commentés et classés.
http://www.geom.umn.edu/software/tilings/TilingSoftware.html
Une page de lien sur les logiciels de pavages.
http://www.ics.uci.edu/~eppstein/junkyard/tiling.html
Les liens sur les pavages du site The Geometry Junkyard. Des liens extrêmement nombreux,
dans lesquels sans doute il convient de faire le tri. Concerne tous les types de pavages,
réguliers ou non.