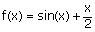 .
. , B
, B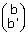 , C
, C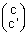 , D
, D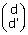 . Les points
M et N sont définis comme intersections de droites.
. Les points
M et N sont définis comme intersections de droites.Double inégalité des accroissements finis |
|
| Groupe Maths&Info 1994, 2000 |
|
Niveau
Terminale S.
Objectifs
Découvrir la double inégalité des accroissements finis à partir
d'une lecture graphique.
La démontrer ensuite.
Prérequis
Lire un encadrement sur un graphique.
Déterminer une équation de droite connaissant l'un de ses points et son coefficient
directeur ; obtenir le coefficient directeur d'une droite définie
par deux points.
Interpréter graphiquement le nombre dérivé d'une fonction en un point.
Déduire le sens de variation d'une fonction dérivable à partir du signe de sa
dérivée.
Logiciel utilisé
GéoplanW version 1 de décembre 96.
Déroulement de la séquence
Distribution de la page 2, courbe représentative d'une fonction
dérivable sur un intervalle donné [ a ; b ],
avec A (a , f(a)) et B (b ; f(b)).
Les élèves ont à tracer un parallélogramme de diagonale [AB] « contenant » ce graphique, puis à obtenir
des encadrements de f(x)
sur [ a ; b ].
Distribution de la page 3. Sur un second graphique muni d'un parallélogramme
imposé, étude de la conservation des encadrements précédents quand on prend
un parallélogramme « analogue » inclus dans [ a ; b ].
Distribution de la page 4. Ŕ partir des essais précédents, découverte de la
condition suffisante sur la dérivée de f pour
que cette conservation ait lieu.
Démonstration de la double inégalité des accroissements finis.
Prolongements : recherche du « meilleur » parallélogramme ; étude
de deux cas de non dérivabilité en un point d'une fonction.
Commentaires pour le professeur
Cette activité a été testée par l'auteur en classe de Terminale
D, sous la version Dos de Géoplan : les paragraphes 1 à 4 ont alors
été traités en une heure dans une salle équipée d'un seul ordinateur muni de
la rétroprojection sur un écran. C'est le professeur qui manipulait Géoplan
en faisant les essais proposés par les élèves.
Les fichiers sont mis à jour pour GéoplanW (version 1 de 96).
Les fichiers g2w associés à cette activité laissent à la disposition de l'utilisateur
toutes les fonctionnalités de GéoplanW. Si on veut mettre ces fichiers dans
les mains des élèves, on peut, pour éviter d'avoir à réparer les maladresses,
ne laisser à disposition que les fonctionnalités strictement nécessaires (articles
"Modifier les menus" et "préférences").
En l'état actuel :
![]() Chaque fichier est assorti d'un
commentaire ou d'une aide grossière (F3).
Chaque fichier est assorti d'un
commentaire ou d'une aide grossière (F3).
![]() Tous les objets de chacune des
figures peuvent être modifiés (icône M/D).
Tous les objets de chacune des
figures peuvent être modifiés (icône M/D).
![]() La fonction f
cachée dans les premiers paragraphes est définie par
La fonction f
cachée dans les premiers paragraphes est définie par 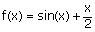 .
.
![]() Les coefficients directeurs des
droites (AM) et (AN) sont p et q respectivement.
Les coefficients directeurs des
droites (AM) et (AN) sont p et q respectivement.
![]() Le repère cartésien utilisé est
r d'origine O. Les points définis par leurs coordonnées dans r sont :
A
Le repère cartésien utilisé est
r d'origine O. Les points définis par leurs coordonnées dans r sont :
A , B
, B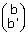 , C
, C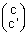 , D
, D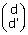 . Les points
M et N sont définis comme intersections de droites.
. Les points
M et N sont définis comme intersections de droites.
Les parallélogrammes sont définis comme polygones, ce qui permet de colorier éventuellement leur intérieur et surtout l'intérieur de celui de diagonale [CD].
1. Encadrement graphique d'une fonction par des fonctions affines
Soit f la fonction dont le graphique (C) est le suivant (figure 1) :
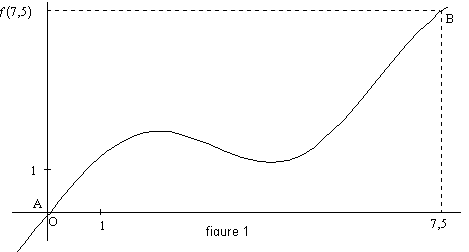
A et B sont les points de (C) d'abscisses respectives a = 0 et b = 7,5.
Tracer sur la figure 1 un parallélogramme AMBN vérifiant les trois conditions suivantes :
« contenant » (C),
dont aucun côté n'est parallèle à la droite des ordonnées,
tel que (AM) soit « au-dessus » de (C)
sur [ a ; b ].
Traduire, par deux encadrements de f(x), les informations ci-dessus en appelant p et q les coefficients directeurs respectifs de (AM) et (AN).
En fonction de a, b, p et q, nous obtenons :
Lire graphiquement, puis déduire, par le calcul, des deux encadrements précédents de f(x), un encadrement du coefficient directeur de (AB).
2. Étude de la conservation des encadrements précédents

Soit [ c ; d ] [ a ; b ] ; C et D les points de (C) d'abscisses respectives c et d.
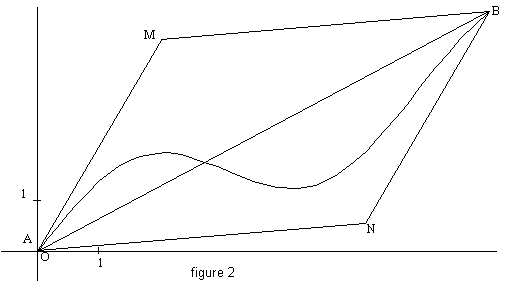
1. Les trois encadrements précédents (1), (2) et (3) sont-ils encore vrais quand a est remplacé par c et quand b l'est par d ?
Indication : avec géoplanW (fichier "accfin1.g2w"), déplacer C ouD.
2. Le parallélogramme que vous avez dessiné sur la figure 1, donne-t-il le même type de résultat (que celui que nous venons d'obtenir) sur la conservation des trois encadrements ?
Indication : avec géoplanW (fichier "accfin1.g2w"), prendre pour p et q les valeurs choisies dans la figure 1, puis déplacer C ou D.
3. Conservation des trois encadrements
Pour que (4), (5) et (6) soient vraies quels que soient les choix faits pour c et d dans [ a ; b ],
Quelle modification de p et q
pent-on proposer ? Essayer plusieurs valeurs de p
et q (avec l'aide de GéoplanW).
Quelle condition suffit-il que p et q
vérifient ?
Quelle condition suffit-il que f' vérifie ?
Quelle valeur minimale de p et quelle valeur maximale de q offrent le « meilleur » parallélogramme de diagonale (AB) ?
4. Démonstration de l'inégalité des accroissements finis
Soit f une fonction numérique d'une variable réelle, dérivable sur un intervalle [ a ; b ].
Supposons que f' est telle que
Donc :
5. Et si, en un point de ] a ; b [, f n'était pas dérivable ?
Étudier sur l'intervalle [ 0 ; 2 ],
les encadrements (1), (2) et (3) pour la fonction définie par : 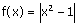 . (fichier
"accfin2.g2w")
. (fichier
"accfin2.g2w")
6. Et si f n'était pas dérivable en a ?
Étudier sur [ 0 ; 2 ], les encadrements (1), (2) et (3) pour la fonction radical. (fichier "accfin3.g2w")