Aire d’un triangle inscrit dans un carré
![]()
Lycée Camille Jullian, Bordeaux
Groupe Math&Info, Bordeaux 2001
Mise à jour : Groupe Maths&Info 2001
Niveau
Première ou terminale S.
Prérequis
1ère S : Sens de variation d'une fonction à partir du
signe de la dérivée ; équation et inéquation du second degré ; équation cartésienne
d'une parabole.
Terminale S : idem (avec paramètres) + éléments caractéristiques d'une parabole.
Objectifs
Faire la liaison entre un problème géométrique et sa traduction
analytique.
Utiliser quelques outils fondamentaux de l'analyse.
Etudier une famille de fonctions (terminale).
Organisation pratique
Ordinateur tableau noir (professeur) avec tablette de rétroprojection
et rétroprojecteur (une utilisation en salle informatique est également envisageable).
Imagiciels airecar1.g2w
(première), airecar2.g2w
(terminale) créés par le professeur et utilisables à l'aide du logiciel géoplanW
du creem.
Durée : 2 h en première S.
Description
L'écran de l’imagiciel est partagé en deux parties :
![]() celle de gauche illustre la situation géométrique (le carré et les variations
des différents points de la figure, les points mobiles pouvant être M
ou I suivant le niveau proposé).
celle de gauche illustre la situation géométrique (le carré et les variations
des différents points de la figure, les points mobiles pouvant être M
ou I suivant le niveau proposé).
![]() celle de droite contient la représentation graphique de la fonction A.
celle de droite contient la représentation graphique de la fonction A.
La parabole P représentant l'ensemble décrit par le point J peut s'obtenir par deux méthodes ; la copie d'écran de l'annexe : Document Professeur montre les tracés de L et P pour deux positions de I (les courbes se modifiant automatiquement par simple appui sur les touches de direction).
Bilan
Cette séance n'a été testée en classe qu'en première
S.
L'extrème souplesse d'utilisation de géoplanW permet de
modifier les fichiers airecar1.g2w et airecar2.g2w
de manière à les adapter très rapidement suivant les objectifs du professeur (2 parties
distinctes dans chaque problème) et le niveau des élèves (première ou terminale).
Les élèves auront sans doute à être guidés pour le calcul de l'aire du triangle : des
factorisations effectuées suffisamment tôt permettent d'éviter des calculs fastidieux.
Auteur
Lycée Camille Jullian, Bordeaux
Groupe Math&Info, Bordeaux 2001
Mise à jour : Groupe Maths&Info 2001
Problème
On donne un carré ABCD de côté 2 cm.
Soit I un point de ]AB[, M un point variable du segment ]BC[, N le point de la droite (CD) tel que le
triangle (IMN) soit rectangle en M, J le milieu de [MN].
Soit E, F et H les milieux
respectifs de [AD], [AB] et [CD]. On
se place dans le repère orthonormé (A, E, F). On
note x l'abscisse du point M.
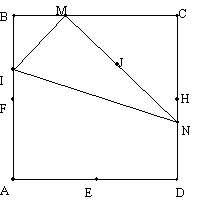
Le but du problème est double :
a. Déterminer les variations de l'aire du triangle (IMN) quand M varie sur [BC].
b. Déterminer le lieu P du point J quand M varie sur [BC].
Version 1 (Niveau première)
On suppose que I = F.
a. Calculer les coordonnées du point N en
fonction de x.
Montrer que, lorsque x varie, N
se déplace sur ]CH], o¨ H est le
milieu de [CD].
b. Déterminer en fonction de x l'aire A(x) du triangle IMN. ╔tudier les variations de la fonction A sur son ensemble de définition.
c. Calculer les coordonnées xJ et yJ du point J en fonction de x. Exprimer yJ en fonction de xJ En déduire que P1, courbe représentative de cette fonction, est une parabole. Préciser les coordonnées de son sommet.
Version 2 (Niveau terminale)
On note m l'ordonnée du point I.
a. Calculer les coordonnées du point N en fonction de x et m.
b. Montrer que, si ![]() , alors,
quelle que soit la position de M sur ]BC[,
N varie entre les points C et
D.
, alors,
quelle que soit la position de M sur ]BC[,
N varie entre les points C et
D.
c. On suppose dans cette question que ![]() .
.
Déterminer en fonction de x et m
l'aire ![]() du triangle IMN.
du triangle IMN.
Montrer qu'il existe un réel m1 de
l'intervalle ![]() tel
que :
tel
que :
(1) pour tout m de l'intervalle
] 0 ; m1 ], la fonction Am est monotone sur son
ensemble de définition ;
(2) pour tout ![]() , l'équation
, l'équation ![]() admet deux solutions x1 et x2, avec
admet deux solutions x1 et x2, avec ![]() .
.
Déduire de ce qui précède le sens de variation de la famille des fonctions Am pour tout m
de l'intervalle ![]() .
.
d. Calculer les coordonnées xJ et yJ du point J en fonction de x et m. Exprimer yJ en fonction de xJ et m. En déduire que Pm, courbe représentative de cette fonction, est une parabole dont on précisera les éléments caractéristiques en fonction du paramètre m.
Document professeur
Version 1 (Niveau première)
Pour faire fonctionner l'imagiciel cliquer sur la figure : celle-ci deviendra alors active ; il est possible de faire apparaître les commentaires à l'aide de la touche F3 et d'utiliser les différentes commandes soit à l'aide des touches du clavier correspondantes, soit à l'aide des boutons.
|
Par défaut le point M est pilotable
au clavier
|
|||
| Ÿ Abscisse x du point M et aire de MNF : A(x) |
|
|
|
| Ÿ Point S de coordonnées : (x, A(x)) |
|
||
| Ÿ Représentation graphique de la fonction A |
|
||
| Ÿ Point J : milieu du segment [MN] |
|
||
| Ÿ Lieu du point J |
|
|
|
Dans le cadre de droite on construit le point S de coordonnées (x, A(x)).
On pourra faire afficher ou non :
Ÿ les valeurs
de x et de A(x)
Ÿ le point S
Ÿ la représentation
graphique de la fonction A
Le tracé de P (lieu du point J) peut s’obtenir de deux fašons :
Ÿ
on passe en mode Trace et en déplašant le point M
on visualise le lieu du point J (appuyer sur Echap pour quitter
le mode Trace).
Ÿ
Appui sur la touche P ou utilisation du bouton d'affichage
: on obtient l’affichage de la parabole.
Version 2 (Niveau terminale)
Pour faire fonctionner l'imagiciel cliquer sur la figure : celle-ci deviendra alors active ; il est possible de faire apparaître les commentaires à l'aide de la touche F3 et d'utiliser les différentes commandes soit à l'aide des touches du clavier correspondantes, soit à l'aide des boutons.
|
Par défaut le point M est pilotable
au clavier
|
|||
| Ÿ Pilotage des points au clavier |
|
||
| Ÿ Abscisse x du point M et aire de MNF : Am(x) |
|
|
|
| Ÿ Ordonnée m du point I |
|
||
|
Ÿ Point
S de coordonnées : (x, Am(x))
|
|
||
| Ÿ Représentation graphique de la fonction Am |
|
||
| Ÿ Point J : milieu du segment [MN] |
|
||
| Ÿ Lieu du point J |
|
|
|
Dans le cadre de droite on construit le point S de coordonnées (x, Am(x)).
On pourra faire afficher ou non :
Ÿ
les valeurs de x et de Am(x)
Ÿ
la valeur de m (ordonnée de I)
Ÿ
le point S
Ÿ
la représentation graphique de la fonction Am
En faisant varier I sur [AB] (classe terminale), ce procédé permet de visualiser la famille des courbes représentatives des fonctions Am.
Le tracé de P (lieu du point J) peut s’obtenir de deux fašons :
Ÿ
on passe en mode Trace et en déplašant le point M
on visualise le lieu du point J (appuyer sur Echap pour quitter
le mode Trace).
Ÿ
Appui sur la touche P ou utilisation du bouton d'affichage
: on obtient l’affichage de la parabole.