Aire maximale à périmètre constant |
|
|
|
Équipe Académique Mathématiques
Bordeaux, janvier 2006 |
|
|
Destination
Professeurs
Niveau
Première L, option facultative, nouveaux programmes.
Type
Papier et TICE (GéoplanW et Tableur)
Fichiers TICE : aire_max.g2w, aire_max.123, aire_max.xls
Extraits du programme
Première L enseignement optionnel
| Contenus |
Modalités |
Commentaires |
| Exemples de problèmes
mettant en jeu des fonctions simples. |
Traduire un problème
en une question portant sur une fonction : Quelle est l’image du
nombre réel a ? … La fonction admet-elle un extremum ?
Conjecturer à partir de l’observation d’une représentation
graphique obtenue à l’aide d’une calculatrice graphique ou d’un logiciel. |
Les fonctions sont à
choisir parmi les fonctions polynômes de degré au plus 3, ou les fonctions
rationnelles du type
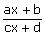 . . |
| Dérivation
Résolution de problèmes à supports variés grâce à
la détermination et à l’étude d’une fonction.
|
Il s’agit :
- d’exploiter les variations d’une fonction pour
prouver l’existence d’un minimum ou d’un maximum sur un intervalle…
. |
Les problèmes abordés seront issus de situations
simples, cinématiques (mouvement d'un point sur un axe gradué), géométriques
(aire d'un rectangle de périmètre donné en fonction d'une dimension, remplissage
d'un récipient), économiques (coût, bénéfice, coût moyen, offre et demande). |
Commentaires
Sur la base d’un texte d’exercice concret l’utilisation du
logiciel GéoplanW permet une visualisation du problème et la conjecture de la
solution recherchée.
À l’aide du tableur il est alors possible d’approcher la solution
en faisant varier l’intervalle de calcul (changement de la valeur initiale)
ainsi que le pas.
Le logiciel GéoplanW permet
ensuite de visualiser une solution algébrique de l’exercice.
Un calcul de dérivée permettra de justifier les différentes
conjectures.
Problème
A l’aide de 75 mètres de grillage, un fermier veut réaliser un enclos
rectangulaire d’aire maximum dans une vaste prairie.
Comment doit-il s’y prendre ?
Modélisation
On note x et y les dimensions du rectangle représentant l’enclos.
Il s’agit de rendre x.y maximum avec x + y = 37,5.
Conjectures à l’aide de GéoplanW et d’un tableur
La figure GéoplanW permet de faire varier la valeur de x au clavier
ou à la souris et de conjecturer la valeur donnant l’aire maximum grâce à l’affichage
de la valeur de cette aire; d’autre part il est possible de faire afficher le
point S de coordonnées ( x , Aire ) ainsi que la courbe représentative de la
fonction aire.
Le tableur permettra d’approcher la solution conjecturée en traçant
la représentation graphique de la fonction aire sur un intervalle dont on pourra
modifier la borne inférieure afin d’obtenir un encadrement de la solution cherchée.
Solution algébrique sans dérivée et visualisation géométrique
avec GéoplanW
Vérifier l’égalité 1/4 ´
(x + y)2 - 1/4 ´
(x - y)2 = xy puis conclure.
Solution avec dérivée
L’aire est égale à : x ´
(37,5 - x) c’est-à-dire : - x2 + 37,5 x etc.
Les outils de la figure GéoplanW : aire_max.g2w
À l'aide d'un grillage de longueur donnée (Clot) , un fermier veut
réaliser un enclos rectangulaire d'aire maximum dans une vaste prairie.
x et y sont les dimensions du rectangle ABCD représentant l'enclos.
La touche 4 permet de fixer la longueur du grillage à 60 m.
La touche 5 permet de fixer la longueur du grillage à 65 m.
La touche 6 permet de fixer la longueur du grillage à 70 m.
La touche 7 permet de fixer la longueur du grillage à 75 m.
La touche 8 permet de fixer la longueur du grillage à 80 m.
La touche 9 permet de fixer la longueur du grillage à 85 m.
Le point l (pilotable au clavier) permet de faire varier la longueur
x entre et Clot/2.
La touche R permet d'afficher un repère dans lequel est placé le point S(x;Aire).
La touche T permet de garder la trace de point S lorsque x varie.
La touche C permet de visualiser le lieu du point S.
La touche D permet d'afficher une figure complémentaire sur laquelle on peut
voir les carrés de côtés x + y et x - y.
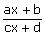 .
.