Niveau

Seconde

Objectifs

Introduire les différentes propriétés des fonctions (parité, périodicité, sens de variation, extremum) et profiter de la situation géométrique pour expliciter les définitions.

Prérequis

Définition d'une fonction.
Courbe représentative d’une fonction.
Orientation du plan.

Organisation pratique

Ordinateur “ tableau noir ” avec sortie sur deux téléviseurs.
Logiciel géoplanW. Une fiche décrivant le problème.
Travail de recherche à la maison suivi d’un cours illustré d’images logicielles.

Description

Les élèves doivent chercher chez eux à représenter graphiquement la fonction définie dans l’énoncé qui leur est distribué. Ils doivent chercher la forme explicite de la fonction quand M est sur [AB].
Le professeur reprend en classe l'énoncé pour les élèves n'ayant pas bien compris l'exercice et utilise géoplanW pour montrer le tracé de la courbe au fur et à mesure que le point M se déplace. Les élèves interviennent pour faire des remarques.
La notion de périodicité est vite sentie, puis la parité et le sens de variation. Toutes les remarques sont justifiées à l'aide des transformations dans le triangle.
Une synthèse termine la séance.

Bilan

Les élèves les plus faibles ont éprouvé des difficultés pour expliciter cette fonction. Ils se sont contentés de mesurer la distance GM.
Cette séance a permis de dégager assez rapidement, et de manière vivante, les notions fondamentales sur les propriétés des fonctions. Les élèves ont pu exprimer seuls leurs définitions.

Enroulement autour d’un triangle

Soit ABC un triangle équilatéral “ direct ” de côté 12 cm, G son centre de gravité (“ direct ” signifie que, pour passer de A à B puis à C en tournant autour du triangle, on tourne dans le sens inverse des aiguilles d’une montre). On dispose d'un fil non élastique gradué en cm de -72 à +72. On enroule ce fil autour du triangle dans le sens direct de telle façon que la graduation 0 soit en A. Tout point d'abscisse x du fil correspond à un point M du triangle. On appelle g l'application qui, à x fait correspondre la distance GM.

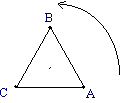1.  Où est M lorsque x vaut 12 ? 36 ? 54 ? -12 ? -48 ? -30 ? -69 ?
2.  Que vaut GM lorsque x vaut 0 ? 12 ? 36 ? 54 ? -12 ? -48 ? -30 ? -69 ?
3.  Calculer GM en fonction de x lorsque x appartient [0,6] puis lorsque x appartient à [6,12].
4.  Construire point par point la portion de courbe représentative de g sur [0,12]
5.  Peut-on prévoir l'allure générale de la courbe ?

Enroulement autour de triangles divers

Quelle est la période si le triangle est isocèle?
Pour illustrer, il suffit d’utiliser la commande CTRL-I qui change la valeur de la constante a2.

Document professeur

Figure préparée avec géoplanW

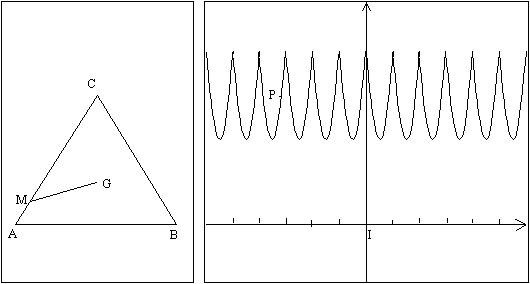
Remarques techniques

La construction de l'imagiciel a nécessité
- la construction de deux cadres A et B
- dans le cadre A
* la construction du triangle équilatéral ABC avec dans le repère nommé R d'origine A : B(1,0) C(0,5;a2)
* la détermination des coordonnées paramétriques de M à l'aide de la fonction µ et des équations paramétriques des droites (AB), (AC) et (BC).
-        dans le cadre B, la détermination du point P de coordonnées (x, GM) dans un repère orthogonal puis le tracé de la courbe en tant que lieu du point P.

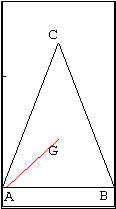
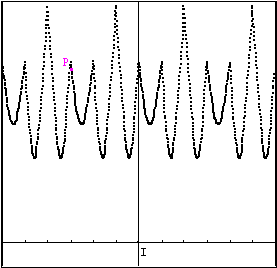
Cas d’un triangle isocèle

La commande CTRL-I permet de transformer le triangle ABC en un triangle isocèle ; la commande CTRL-E permet de revenir à un triangle équilatéral.