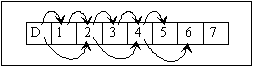
Approche exponentielle de la suite de Fibonacci |
|
| Groupe Maths&Info, Bordeaux |
|
Niveau
Terminales ES, S.
Objectifs
Utiliser un tableur et un traceur de courbes pour approcher expérimentalement une suite de Fibonacci par une fonction exponentielle de forme générale exp(ax + b).
Prérequis
Fonctions logarithmes et exponentielles, suites géométriques.
Cet exercice est prévu pour Works mais peut être utilisé avec Excel.
Les élèves doivent connaître les adressages relatifs, les copies directionnelles
et l'usage élémentaire du grapheur.
Organisation pratique
L'activité peut être faite en travaux dirigés ou en utilisant l'ordinateur comme « tableau noir ».
Description
Voir document professeur.
Bilan
Le problème consiste à trouver une expression, en fonction
de n, du terme général de la suite de Fibonacci (f(1) = 1, f(2) = 2 et, pour
n entier plus grand que 2, f(n) = f(n - 1) + f(n - 2)).
Le tableur permet une exploration numérique de la suite, avec mise en images,
puis de conjecturer, en la visionnant, sa nature exponentielle. Il permet ensuite
d'approximer expérimentalement cette suite par une fonction g(n) =e an + b. Reste à justifier par la théorie les observations effectuées.
Cette façon de procéder motive l'élève pour trouver l'expression de f(n).
Le travail se termine par une mise en garde contre l'interprétation hâtive de
résultats fournis par une calculatrice ou un tableur.
Auteur
Groupe Maths&Info, Bordeaux
Activité crée lors du stage CAFIP 1990/1991, puis remaniée.
Présentée dans la brochure "Faire des mathématiques au lycée avec l'ordinateur"
Document professeur
Le Problème
Un dresseur de puces a appris à Julie, sa puce préférée, à se déplacer de case en case sur une marelle rectiligne (voir fiche élève). Mais la puce avance aléatoirement tantôt d'une case, tantôt de deux. Il s'agit de dénombrer le nombre de chemins, f(n), lui permettant d'arriver à une case donnée, n.

Organisation du travail
1) Faire créer une feuille de calcul permettant de dénombrer les
chemins conduisant à une case donnée. Faire constater que, pour atteindre la
case n, il faut se trouver soit sur la case n - 1,
soit sur la case n - 2.
En déduire que, si f(n) désigne la fonction cherchée, on peut écrire la relation
: f(n) =
f(n - 1)
+ f(n - 2).
Faire représenter graphiquement le nombre de solutions ; amener les élèves à
conjecturer la nature de la croissance.
Faire vérifier les conjectures en passant au logarithme ou en graduant l'axe
des ordonnées de façon logarithmique.
2) Faire rechercher expérimentalement une fonction h(x) = ax + b approchant "au mieux" la fonction ln(f). Cette activité fait bien "sentir" le rôle des coefficients a et b dans l'allure de la droite d'équation y = ax + b. En déduire que f(n) est à peu près égal à eax + b.
3) Faire chercher l'expression exacte de f en fonction de n et interpréter le résultat trouvé précédemment.
4) Montrer qu'un tableur (ou une calculatrice) c'est bien mais qu'il faut faire attention...
Utilisation du tableur
| 1 |
2 |
|
| 1 |
Problème du saut de puce |
|
| 2 |
||
| 3 |
numéro des cases |
nombre de chemins |
| 4 |
0 |
0 |
| 5 |
1 |
1 |
| 6 |
2 |
2 |
| 7 |
=L(-1)C+1 |
= L(-1)C+L(-2)C |
| 8 |
Seules les notions de base sont nécessaires :
Entrée de libellés
"Problème du saut de puce " en L1C1
"numéro des cases" en L3C1
"Nombre de chemins" en L3C2
Formatage des colonnes 1 et 2 en largeur
Entrée de nombres 1 en L5C1 et en L5C2
Entrée de formules
=L(-1)C+1 en L7C1 (on
ajoute 1 à la valeur contenue dans la case au dessus afin d'obtenir la suite
des nombres entiers),
=L(-1)C+L(-2)C en L8C2 (on
fait la somme des deux cases au dessus afin d'obtenir le terme suivant de la
suite de Fibonacci).
Notion d'adressage absolu et relatif ; commande "Recopier vers le bas".
Passage au mode graphique
Saisie des séries d'abscisses et d'ordonnées
Choix du type de graphique
Affichage du graphique
Mise en forme
Conjectures sur la forme de la courbe
Laisser la recherche se dérouler. Il est probable que certains pensent à la courbe représentative d'une fonction polynôme. On peut, si nécessaire, les aider à construire la courbe qu'ils souhaitent (calculs de valeurs en colonne 3, qui devient la deuxième série d'ordonnées ; comparaison des deux courbes en les faisant afficher).
Il est (presque seulement, hélas) certain que le mot exponentielle sera prononcé. Pour mettre cette croissance en évidence on fait construire la représentation de ln(f(n)). On peut faire constater, en explorant les options, qu'il est possible de graduer l'axe des ordonnées de façon logarithmique. Faire afficher le graphique et demander aux élèves d'en tirer les conséquences. On appellera D la "droite" obtenue.
Bien préciser qu'il ne s'agit pas d'une droite, que la fonction f est une suite.
Approximation expérimentale de f
1) ln(g(n))=an+b donc g(n)=ean + b
2) Écrire "a=" dans la
cellule à droite de la cellule L2C4.
Nommer a la cellule L2C4.
Écrire "b="
dans la cellule à droite de la cellule L3C4.
Nommer b la cellule L3C4.
Faire afficher en colonne 4 les valeurs de an+b et en colonne 5 les valeurs de exp(an+b)
en correspondance avec les valeurs de n de la colonne 1. Pour commencer, prendre
a=1 et b=0.
Il est nécessaire d'introduire la notion de recopie en mode absolu (forme $a).
Faire créer un graphique avec,
* pour série d'abscisses, les valeurs de n,
* pour première série d'ordonnées, les valeurs de ln(f(n)),
* pour deuxième série d'ordonnées, les valeurs de an + b.
En faisant varier a, approcher au plus près la direction de D.
On constate sur le graphique ci-dessus que pour a = 1, le coefficient directeur de la droite D', représentative de y = an + b (ou y = ln(g(n))), est environ deux fois trop grand. Il convient donc d'essayer 0,5 puis d'affiner.
Une fois obtenues deux droites sensiblement parallèles, on fait varier b en commençant par -1 (par exemple).
On constate que la droite D' est au dessous de D donc qu'il faut prendre b légèrement supérieur. Un essai à -0,5 puis à -0,4 où D' est au dessous de D amène à choisir b = -0,3.
Expérimentalement, a = 0,48 et b = 0,3 semblent convenir.
Recherche de f(n) en fonction de n
La recherche de la forme fonctionnelle d'une suite à deux pas du type Fibonnacci peut prendre diverses formes. En terminale on peut chercher les suites géométriques vérifiant la relation de récurrence (1) un = un - 1 + un - 2.
L'équation en q, qn = qn - 1 + qn - 2 , amène à résoudre l'équation q2 = q + 1 qui possède deux solutions, (1 + racine(5))/2 et (1 - racine(5))/2, soit le nombre d'or, q, et l'opposé de son inverse, -1/q. Il existe donc deux suites géométriques de premier terme 1, vérifiant la relation (1).
Il est immédiat que toute combinaison linéaire de ces suites vérifie aussi la relation de récurrence. On cherche alors la suite, v, de la forme cqn + d(-1/q)n qui vérifie v0 = 1 et v1 = 1. On en déduit que f(n) = vn.
On constate que, quand n croît, la suite géométrique dont la raison est -1/q tend très vite vers 0. On a donc très vite f(n) à peu près égal à cqn. C'est pourquoi, dès que n augmente (n > 10), on est très près d'une exponentielle.
Par suite an + b = ln(cqn) et donc a = ln(q) et b = ln(c). On trouve a = 0,481211... et b =-0,323507...
Mise en garde
Le calcul de un, à l'aide du tableur, pour u0 et u1 quelconques ne pose pas de problème. Il suffit de modifier les valeurs convenables sur la feuille de calcul. Mais on constate que pour certaines valeurs de départ (exemple : u0 = 2 et u1 = (1 - rac(5)), le tableur "déraille", tout comme d'ailleurs le ferait une calculatrice. Dans ce cas, la suite f est la suite géométrique de premier terme 2 et de raison (1 - rac(5)) / 2. Elle converge vers 0...
| n |
un |
| 0 |
2 |
| 1 |
-1,2360679775 |
| 2 |
0,7639320225 |
| 3 |
-0,472135955 |
| 4 |
0,2917960675 |
| 5 |
-0,1803398875 |
| 6 |
0,11145618 |
| 7 |
-0,068883707497 |
| 8 |
0,042572472504 |
| 9 |
-0,026311234993 |
| 10 |
0,016261237512 |
| 11 |
-0,010049997481 |
| 12 |
0,0062112400303 |
| 13 |
-0,003838757451 |
| 14 |
0,0023724825792 |
| 15 |
-0,0014662748718 |
| 16 |
0,00090620770746 |
| 17 |
-0,00056006716432 |
| 18 |
0,00034614054314 |
| 19 |
-0,00021392662117 |
| 57 |
-3,9701735012E-05 |
| 58 |
-6,423875119E-05 |
| 59 |
-0,0001039404862 |
| 60 |
-0,00016817923739 |
| 61 |
-0,00027211972359 |
| 90 |
-312,89713588 |
| 91 |
-506,27820084 |
| 92 |
-819,17533673 |
| 93 |
-1325,4535376 |
| 94 |
-2144,6288743 |
| 95 |
-3470,0824119 |
Document élève
Situation
Un dresseur de puces a appris à Julie, sa puce préférée, à se déplacer de case en case sur une marelle semblable à la suivante, la case départ pouvant être numérotée 0 :
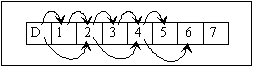
La puce, d'humeur facétieuse, avance aléatoirement, à chaque saut, d'une ou deux cases, sans jamais reculer. Au début elle se trouve sur la case départ.
Exemples : Les chemins possibles pour aller à
On aimerait pouvoir dire directement combien de chemins conduisent à une case donnée, n. Avant de lire la suite essayez, pendant quelques minutes, de trouver combien de chemins arrivent aux cases 3, 4, 5 ? Sauriez-vous automatiser ce calcul ?
Problème
Soit f la fonction donnant, en fonction
de n, le nombre de possibilités d'atteindre la case numéro n. Compte tenu des
hypothèses, on sait que f(1) = 1, f(2) = 2. Montrez que, si f(n) désigne
la fonction cherchée, on peut écrire, pour 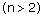 , la relation
, la relation
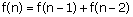
Cette relation permet de calculer f(3), f(4) et, de proche en proche, f(n). Mais on préférerait avoir l'expression de f en fonction de n.
Vous allez d'abord étudier expérimentalement, à l'aide du tableur, des propriétés de la fonction f : f est-elle, ou ressemble-t-elle à une fonction connue ? quel est son comportement lorsque n croît ?
Vous déterminerez ensuite f(n) en fonction de n et essaierez de justifier les observations que vous aurez faites dans la partie précédente.
Enfin ce TP vous montrera qu'il faut se méfier des outils de calcul approché (calculatrices, ordinateurs, . . . ) et que, par conséquent, toute observation effectuée avec ces outils doit nécessairement, pour être validée, être étayée par une démonstration.
Étude expérimentale
1. Créez une feuille de calculs comportant :
Notes techniques :
la fonction logarithme népérien (ln) s'écrit LOG sous
Works ;
utilisez la commande "recopie vers le bas" ;
faites le calcul pour les trente premières cases, vous pourrez aller plus
loin ensuite par une simple recopie vers le bas.
2. Avec l'option graphique de Works, représentez f
pour n variant de 1
à 10, puis de 1 à 20, et enfin de 1 à 30.
Est-il
naturel de choisir le format "courbe" pour représenter f ?
Que pouvez vous conjecturer quant à la nature de la croissance ?
3) Représentez graphiquement la fonction ln(f)
(couples (n, ln(f(n)))
pour n variant de 1 à 10, puis de 1 à 20 et enfin de 1 à 30.
Que pouvez-vous
conjecturer quant à la nature de cette courbe ?
4) Si 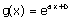 ,
a et b étant deux
réels donnés, que peut-on dire de la fonction ln(g) ?
,
a et b étant deux
réels donnés, que peut-on dire de la fonction ln(g) ?
5) Dans cette question vous allez montrer que, lorsque n
croît. f peut être "approchée" par une fonction g dont vous déterminerez expérimentalement les coefficients
a et b.
Insérez dans votre feuille de calcul quatre lignes avant la ligne 1. Nommez
a la cellule L1C4 et b la cellule L2C4.
Faites afficher en colonne 4 les valeurs de an + b
et en colonne 5 les valeurs correspondantes de g(n).
Commencez avec les valeurs a = 1 et b = 0.
Faites afficher, simultanément, les représentations graphiques de ln(f)
et ln(g) pour n variant de 1
à 20. Bien que f soit une suite, il est avantageux de relier les points
(n, f(n)) pour mieux voir les points. La courbe représentative
de la fonction ln(f) est presque une droite, celle
de la fonction ln(g) en est une.
Comparez les coefficients directeurs des deux "droites" affichées.
Qu'en déduisez-vous ?
Modifiez convenablement les valeurs de a afin d'obtenir des droites parallèles.
Affinez les valeurs de a et b en faisant varier b, puis
de nouveau, éventuellement, a et b, jusqu'à la confusion des deux "droites".
Représentez alors sur un même diagramme les courbes des fonctions f et g et donnez l'expression
de g.
Étude théorique
Une suite qui croît de manière approximativement exponentielle est, à peu de chose près, une suite géométrique.
1) Déterminez les suites géométriques vérifiant : 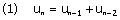
Soient q et q'
les raisons de ces suites. On appelle q celle
qui est positive.
Montrez que, pour tout couple (c, d) de x, la suite v, définie par 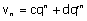 ,
vérifie (1).
,
vérifie (1).
2) Déterminez les valeurs de c et d pour 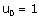 et
et 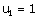 .
Comparez f avec la suite ainsi obtenue.
.
Comparez f avec la suite ainsi obtenue.
3) Montrez que, quand n tend vers l'infini, la suite 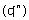 tend vers
0.
tend vers
0.
En déduire les "meilleures" valeurs de a et b pour l'étude expérimentale.
Vérifiez avec le tableur.
Méfiance !
Une suite obéissant à la relation de récurrence 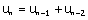 est définie
dès que l'on connaît ses deux premiers termes. Supposons que ces termes soient
est définie
dès que l'on connaît ses deux premiers termes. Supposons que ces termes soient
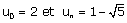 .
.
Calculez 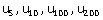 .
Que suggère le tableur ?
.
Que suggère le tableur ?
Et pourtant. . .
Démontrez que dans ce cas la suite est en fait la suite géométrique
de premier terme 2 et de raison ![]() .
Quelle est donc par conséquent sa limite ?
.
Quelle est donc par conséquent sa limite ?
Peut-on
se fier aveuglément à un tableur (ou d'ailleurs à une calculatrice car les méthodes
de calcul sont semblables) ?