La ficelle élastique

Équipe Académique Mathématiques, Bordeaux
janvier 2006

 

Destination

Professeurs

Niveau

Première et Terminale L, option facultative, nouveaux programmes

Type

Papier et TICE (GéoplanW + tableur) ; fichier ficelle.g2w

Extraits du programme

Première L enseignement optionnel

Contenus

Modalités

Commentaires

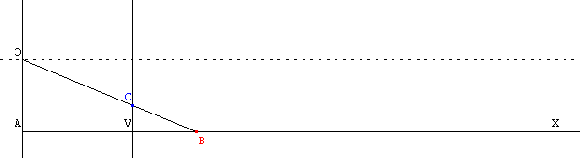
Exemples de problèmes mettant en jeu des fonctions simples.

Conjecturer à partir de l’observation d’une représentation graphique obtenue à l’aide d’une calculatrice graphique ou d’un logiciel.

Les fonctions sont à choisir parmi les fonctions polynômes de degré au plus 3, ou les fonctions rationnelles du type

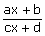
(ax+b)/(cx+d)

Dérivation

 

Nombre dérivé d'une fonction en un réel ; définition comme limite du taux d’accroissement…

 

 

 

 

 

 

 

 

Résolution de problèmes à supports variés grâce à la détermination et à l’étude d’une fonction.

 

 

Des éclairages différents du nombre dérivé sont à donner durant l’année :

- approximation affine

- géométrique

- cinématique.

 

 

 

La définition formelle de la notion de limite n’est pas au programme. Le vocabulaire et la notation relatifs aux limites seront introduits à cette occasion, mais uniquement sur des exemples.

Tangente à la courbe représentative.

Vitesse instantanée d’un mobile animé d’un mouvement rectiligne.

 

Les problèmes abordés seront issus de situations simples, cinématiques (mouvement d'un point sur un axe gradué), géométriques (aire d'un rectangle de périmètre donné en fonction d'une dimension, remplissage d'un récipient), économiques (coût, bénéfice, coût moyen, offre et demande).

 

Commentaires

Sur la base d’un problème historique l’utilisation du logiciel GéoplanW permet une visualisation de la notion de limite et d’asymptote à une représentation graphique.

 

Problème

Le point B est mobile sur la demi-droite [VX) ; le point O est fixe et le segment [OB] est infiniment étirable.
Soit C le point d'intersection du segment [OB] et de la perpendiculaire en V à la demi-droite [VX).
On cherche à visualiser et à modéliser le déplacement du point C sur cette perpendiculaire.

figure

Modélisation

On pose x = VB et on calcule VC en fonction de x sous la forme VC = h(x).
On peut ensuite étudier la limite de la fonction h lorsque x tend vers +¥.
On pourra aussi déterminer le nombre dérivée h’(0) et en déduire la tangente à la représentation graphique de la fonction h à l’origine du repère.

Les commandes de la figure GéoplanW : ficelle.g2w

Pour cela à partir d'un point R placé sur cette perpendiculaire on construit un repère dans lequel on placera en ordonnée la distance VC et en abscisse la distance VB.
La touche C permet de construire pas à pas la figure à partir du point O et des droites de base.
La touche T permet d'obtenir le trace du point S ainsi construit.
La touche A permet de tracer l'asymptote à la trace du point S.
La touche G permet de tracer la tangente en R à la trace du point S.