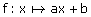 , aet
bétant des nombres réels donnés.
, aet
bétant des nombres réels donnés.Et vogue la galère ! |
Lycée Albert Claveille, Périgueux |
Niveau
Seconde, première STI.
Objectifs
— Trouver rapidement, par simple lecture graphique sur papier quadrillé, une équation de droite (représentation graphique d’une fonction affine).
— Calcul mental sur les fractions et les proportions.
Prérequis
Les fonctions affines ont été abordées au collège.
En seconde, les généralités sur les fonctions ont été traitées (image, antécédent, sens de variation). Les élèves ont eu un premier contact avec Géoplan (réalisation de figures), non nécessaire pour effectuer cette activité.
Description
Le lycée dispose d’une salle informatique équipée de dix-sept machines en réseau et d’un vidéoprojecteur. La vétusté des locaux rend impossible, dans les salles de classes, l’utilisation d’un système ordinateur + vidéoprojecteur, ce qui impose de travailler en salle informatique. L’activité décrite ici est bâtie en fonction de ces contraintes.
Dans leur très grande majorité nos élèves, plus à l’aise avec la pratique qu’avec la théorie, se destinent aux sections STI.
Cette activité est l’aboutissement d’activités similaires menées les années précédentes en classe de seconde et de première STI.
La version présentée ici a été réalisée dans le cadre d’un projet d’établissement Math & TICE en classe de seconde. Dans ce cadre, les élèves disposent, par groupe et par semaine, d’une demi-heure supplémentaire de maths. Les heures dédoublées sont placées en parallèle avec les TP de physique. Sur l’année les élèves assistent à une quinzaine de séances de une heure trente en salle informatique (une séance tous les quinze jours environ), le rythme n’étant pas forcément régulier (disponibilité de la salle, articulation des activités avec le cours).
Cette activité est la cinquième de l’année en salle informatique. Les élèves ont déjà travaillé sur SAMAO (premier contact avec l’ordinateur) et Géoplan. Elle vise à rendre les élèves capables de trouver rapidement, par simple lecture graphique, l’équation d’une droite dessinée sur une feuille quadrillée tout en les obligeant à un minimum de calcul mental sur les fractions : il s’agit de reproduire, à l’aide de Géoplan, un bateau, puis de l’animer.
— Deux semaines avant le TP, un premier travail préparatoire sur les fonctions affines est donné. À faire à la maison et commenté en classe, il vise à mettre en évidence l’invariant Dy/Dx ainsi que l’utilisation graphique que l’on peut en faire pour placer des points d’une droite relativement à des points connus. Ce travail sert d’introduction au cours sur les fonctions affines et les fonctions de référence. En classe, la méthode de lecture des équations de droites est présentée.
— Un deuxième travail préparatoire précède immédiatement la séance en salle informatique. Il s’agit de déterminer les fonctions intervenant dans l’image fournie et l’ensemble de définition de chacune de ces fonctions.
Parallèlement l’étude des fonctions de référence se poursuit.
— Une première séance (une heure trente) en salle informatique permet de vérifier les résultats trouvés. Les élèves sont très surpris de leurs erreurs (coefficient directeur opposé ou inversés, ordonnées à l’origine inexactes, équations « approchées » qui ne conviennent pas et ne résistent pas au « zoom » sur les parties en cause). Les plus rapides commencent à explorer l’animation de la figure.
Parallèlement, en cours, l’étude des fonctions de référence se poursuit. Les fonctions sinus et cosinus sont abordées. Pour réaliser l’animation il suffit de savoir que ces fonctions prennent leurs valeurs dans l’intervalle [ -1 ; 1 ].
— Une deuxième séance (une heure trente) en salle informatique permet de voir les méthodes d’animation de la figure : agir sur tous les coefficients directeurs et toutes les ordonnées à l’origine avec tous les problèmes que cela pose ; utilisation de plusieurs repères...
Dans un premier temps, le professeur traite le sujet au vidéoprojecteur. Il dirige la séance, canalise les idées des élèves et effectue les manipulations.
Dans un deuxième temps les élèves font leurs essais. Un fichier (galmobxx) dont il ne reste à modifier que quelques éléments leur est fourni.
— Une troisième séance est proposée pour permettre aux élèves de finir leur travail et de réaliser leur propre dessin mis au point au préalable à la maison.
— Dans les jours qui suivent les élèves mettent au propre leur compte-rendu. Après contrôle de ce travail le professeur fait la synthèse en classe.
— Quelques temps après une interrogation écrite portant sur des lectures d’équations de droites permet de contrôler les acquis.
Bilan
Comme d’habitude, beaucoup sont ravis de travailler en salle informatique. De nombreux élèves moyens se piquent au jeu et accrochent. Mais tous trouvent moins drôle d’avoir un travail à rendre.
Lors de la première séance en salle informatique, de nombreuses surprises attendent les élèves :
- mauvais choix des intervalles de définition ;
- mauvaises valeurs pour a ou b ;
- utilisation de valeurs approchées à la place de fractions ; conséquence : des segments ne se « touchent » pas ;
Le réseau et le vidéoprojecteur permettent de commenter devant le groupe les erreurs les plus instructives.
Les ordonnées à l’origine qui ne « tombent pas juste » et qui ont été remplacées par des valeurs approchées, donnent l’occasion de montrer la différence entre valeurs exactes et valeurs approchées et de faire du calcul mental sur les proportions.
Des problèmes en apparence simples, ne le sont pas du tout pour nos élèves :
«Quel est le coefficient directeur d’une droite si, partant d’un point de la droite, je retombe sur un point de la droite en portant 3 unités dans le sens des x croissants et 2 unités dans le sens des y croissants ? »
« Sachant que cos t varie entre -1 et 1, trouver une fonction qui varie entre -2 et 2, entre 0 et 2,… »
Les élèves ont du mal à calculer de tête le produit d’une fraction simple (2/3) par un nombre (2), ou de deux nombres simples (12 ´ 3) (méfait d’un usage abusif de la calculatrice ?).
L’animation suscite beaucoup d’intérêt mais peu d’élèves sont capables de la réaliser seuls, même après la présentation par le professeur, et avec le fichier fourni.
L’activité libre est l’occasion de souligner l’importance du choix d’un repère en fonction du dessin à réaliser (centre de symétrie, axe de symétrie).
Certains élèves manquent d’imagination. D’autres au contraire débordent d’inventivité : réalisation d’un téléphérique qui se déplace sur un câble incliné (teleph.g2w), hors bord crachant des flammes (horsbord.g2w), petit chien avançant par bonds,…).
Cette activité prend du temps. En vaut-elle la peine ? Il faudrait le demander aux élèves dans quelques années. Beaucoup ont apprécié mais il reste toujours quelques élèves réfractaires à tout effort, qui expérimentent au hasard, sans réflexion, et ne retiennent rien de ce qu’ils ont fait.
Fiche élève
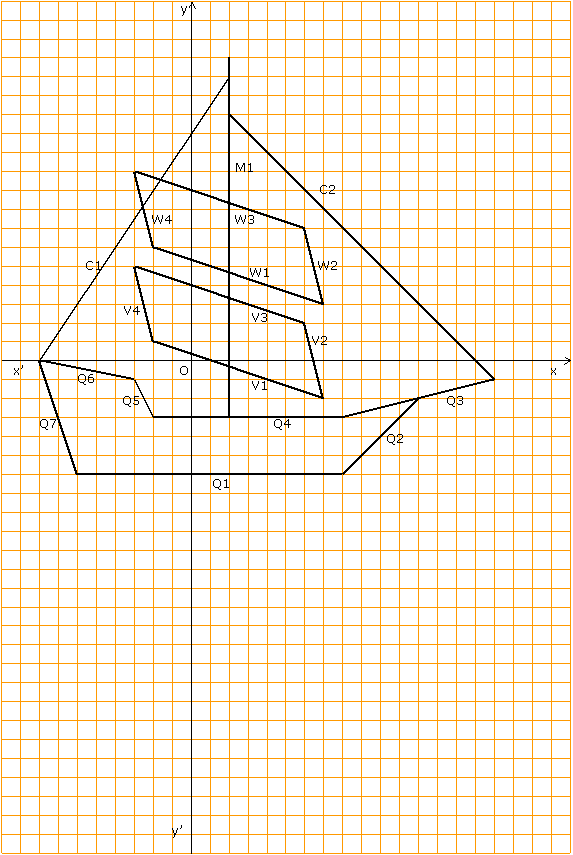
Il s’agit, à l’aide du logiciel Géoplan et en utilisant les fonctions affines, de reproduire le bateau représenté plus loin.
Ce bateau est stylisé à l’aide de segments nommés chacun par une lettre et un chiffre :
¤ Q1, Q2, … pour la coque
¤ V1, V2, … pour la première voile
¤ W1, W2, … pour la deuxième voile ;
¤ M1, M2, … pour les mats ;
¤ C1, C2,… pour les cordages ;
¤ …
Chaque segment, sauf exception que l’on précisera, est la courbe représentative d’une fonction affine définie sur un intervalle I.
Une fonction affine est une fonction du type 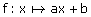 , aet
bétant des nombres réels donnés.
, aet
bétant des nombres réels donnés.
Ici, pour chaque fonction il faut trouver a, b et l’intervalle I
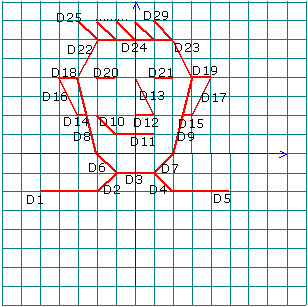
Une fois le bateau terminé, on pourra reproduire, dans un autre fichier Géoplan, la tête du capitaine.
Rédiger un compte rendu de l’activité en répondant clairement aux
questions repérées par le logo  .
.
1 ![]() Qu’est-ce qu’une fonction affine ?
Donner trois exemples de fonctions affines et trois exemples de fonctions non
affines.
Qu’est-ce qu’une fonction affine ?
Donner trois exemples de fonctions affines et trois exemples de fonctions non
affines.
Qu’est-ce qu’une fonction linéaire ? Donner trois exemples de fonctions linéaires et trois exemples de fonctions non linéaires.
On sait que la courbe représentative d’une fonction affine est une droite. Quelle est la particularité de la courbe représentative d’une fonction linéaire ?
On donne la fonction f définie par f(x) = 3 x - 4.
x s’appelle la variable.
f(x) est l'image de x par f. C'est la « valeur de la fonction pour la valeur x de la variable ». Il arrive que l’on note y la valeur de la fonction.
Lorsqu’on passe de x = 1 à x = 3, on dit que la variable « varie » de Dx = +2. Si on passe de x = 4 à x = 1, Dx = -3.
Lorsqu’on passe de x = 1 à x = 3, la fonction varie de Dy = f(3) - f(1) = 10 - 4 = 6.
D désigne la lettre grecque « delta » majuscule.
Dx se lit « delta x ».
2 ![]() Reproduire et compléter le tableau
suivant pour f(x) = 3 x - 4,
puis pour
Reproduire et compléter le tableau
suivant pour f(x) = 3 x - 4,
puis pour
f(x) = -2 x + 3, puis pour f(x) = a x + b, a et b
étant deux nombres réels donnés.
| Valeur initiale de x : 3. Valeur correspondante de la fonction : ……… |
||||
| valeur finale de x |
f(x) |
Dx |
Dy |
Dy / Dx |
| 4 |
||||
| 5 |
||||
| 9 |
||||
| 30 |
||||
| 2 |
||||
| 0 |
||||
| -2 |
||||
Que peut-on dire des suites de nombres des colonnes Dx et Dy ?
3 ![]() On suppose que f(x) = 3 x - 4, que le
plan est rapporté à un repère orthonormal d’unité un carreau, que l’axe des
abscisses est horizontal et orienté vers la droite et celui des ordonnées vertical
et orienté vers le haut. On appelle (D) la droite représentant f.
On suppose que f(x) = 3 x - 4, que le
plan est rapporté à un repère orthonormal d’unité un carreau, que l’axe des
abscisses est horizontal et orienté vers la droite et celui des ordonnées vertical
et orienté vers le haut. On appelle (D) la droite représentant f.
Sur une feuille quadrillée, tracer au centre, à l’intersection de deux lignes du quadrillage, un point A. On suppose que ce point est le point de coordonnées ( 3 ; f(3)). Sans représenter le repère, tracer les points de (D) d’abscisses 4, 5, 9, 2, 0, -2.
Même travail pour f(x) = -2 x + 3.
4 ![]() Sur le quadrillage ci-dessous,
on a A (3 ; 2), B (6 ; 4). Les points C, D, E, F et
G sont sur la droite (AB) et ont tous des abscisses entières. Quelles sont leurs
coordonnées ?
Sur le quadrillage ci-dessous,
on a A (3 ; 2), B (6 ; 4). Les points C, D, E, F et
G sont sur la droite (AB) et ont tous des abscisses entières. Quelles sont leurs
coordonnées ?
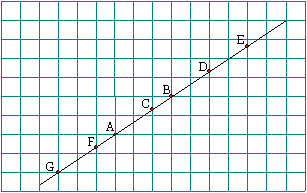
5![]() Mêmes questions si A (-3 ; 4) et B (2 ; 1) ?
Mêmes questions si A (-3 ; 4) et B (2 ; 1) ?
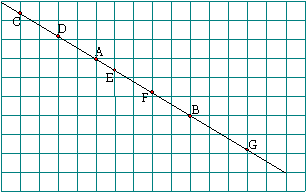
NB : Sur le dessin fourni, les extrémités des segments ont toutes des coordonnées entières.
6 ![]() Un ou plusieurs des segments
proposés ne représentent pas une fonction affine. Préciser lequel ou lesquels
en expliquant pourquoi.
Un ou plusieurs des segments
proposés ne représentent pas une fonction affine. Préciser lequel ou lesquels
en expliquant pourquoi.
7 ![]() En lisant directement sur le
dessin les paramètres a et b de chaque fonction,
reproduire et compléter le tableau ci-dessous (respecter l’ordre alphabétique
pour donner les caractéristiques de chaque segment : A1, A2, …, C1, C2,
…, M1, M2, …, Q1, Q2, … , V1, V2, … , W1, W2, … (les noms des segments peuvent
différer suivant le dessin fourni) et mettre une croix dans le tableau lorsque
le segment n’est pas la courbe représentative d’une fonction affine. La dernière
colonne sera utilisée lors du passage sur le logiciel pour des corrections éventuelles.
En lisant directement sur le
dessin les paramètres a et b de chaque fonction,
reproduire et compléter le tableau ci-dessous (respecter l’ordre alphabétique
pour donner les caractéristiques de chaque segment : A1, A2, …, C1, C2,
…, M1, M2, …, Q1, Q2, … , V1, V2, … , W1, W2, … (les noms des segments peuvent
différer suivant le dessin fourni) et mettre une croix dans le tableau lorsque
le segment n’est pas la courbe représentative d’une fonction affine. La dernière
colonne sera utilisée lors du passage sur le logiciel pour des corrections éventuelles.
| Segment |
Expression de la fonction |
Intervalle de définition |
Correction de la fonction |
Correction de l’intervalle |
| A1 |
||||
| A2 |
||||
| … |
Avec le logiciel Géoplan, il s’agit maintenant de réaliser le dessin proposé. On utilisera les noms portés sur le dessin pour nommer les courbes dans le logiciel).
8 ![]() En fin de TP on réalisera et
animera un dessin libre.
En fin de TP on réalisera et
animera un dessin libre.
Réaliser sur une feuille de papier quadrillé un dessin à l’aide de fonctions affines (il faudra reproduire ce dessin à l’aide du logiciel). Déterminer comme ci-dessus les fonctions.
Le logiciel permet de tracer sur un intervalle la courbe représentative de n’importe quelle fonction.
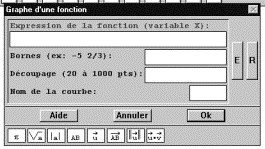
Créer / Ligne / Courbe / Graphe d’une fonction :
Dans la boîte de dialogue on précise :
| ¤ l’expression de la fonction en utilisant la lettre X (majuscule) pour variable muette (ex. : 2X + 1) ¤ les bornes de l’intervalle de définition, séparées par un espace (ex. : -4 2 désigne l’intervalle [ -4 ; 2 ] ) ¤ le nombre de points à calculer (indiquer 20) ¤ le nom de la courbe (le logiciel impose de nommer tous les objets qu’on définit ; il distingue entre majuscules et minuscules). |
 |
Normalement deux points suffisent à un élève pour tracer une droite, mais le logiciel « ignore » qu’il s’agit de droites…
| L’icône Bis ou la combinaison de touche Ctrl B, rappellent la boîte de dialogue de la dernière création. |
 |
 |
La commande Divers / Modifier, dupliquer (accessible par le menu ou par la combinaison de touches Ctrl M) permet de modifier un objet déjà créé (indiquer le nom de l’objet à modifier). La commande Divers / Supprimer permet de supprimer des objets indésirables en les choisissant dans une liste. Pour tracer un segment qui n’est pas la courbe représentative d’une fonction affine, on définit les extrémités de ce segment en indiquant les coordonnées et un nom (Créer / Point / Point repéré / Dans le plan), puis on trace le segment (Créer / Ligne / Segment). On peut tracer plusieurs segments d’un seul coup en espaçant leurs noms : par exemple AB BC CA, pour tracer le triangle ABC, si les points A, B, C ont été définis au préalable. |
Le navire :
La tête du capitaine :
Ce serait tellement mieux si le bateau bougeait !
9![]() On donne la droite d’équation
y = a x + b,
a et b étant deux nombres
réels donnés.
On donne la droite d’équation
y = a x + b,
a et b étant deux nombres
réels donnés.
Sur quel paramètre faut-il agir pour faire « monter ou descendre » la droite sans toucher à son inclinaison ?
Application : on sait que, lorsque le réel t varie, cos t varie entre -1 et 1.
¤ Créer une nouvelle figure (Fichier / Nouvelle figure)
¤ Définir t comme « variable réelle libre » (Créer / Numérique / Variable réelle libre )
¤ Définir le segment d’équation Y = 0.5 X + 3 + cos(t) sur l’intervalle [ -2 ; 4 ].
¤ Rendre t pilotable au clavier (Piloter / Piloter au clavier) et appuyer sur les flèches droite ou gauche…
10![]() Que faudrait-il faire pour
que l’ordonnée à l’origine oscille entre 1 et 5 ? entre 0 et 6 ? entre
0 et 3 ?
Que faudrait-il faire pour
que l’ordonnée à l’origine oscille entre 1 et 5 ? entre 0 et 6 ? entre
0 et 3 ?
On veut maintenant donner une impression de tangage : l’inclinaison de chaque segment augmente puis diminue, puis augmente de nouveau…
11 ![]() Sur quel paramètre de l’équation
y = a x + b faut-il
agir ?
Sur quel paramètre de l’équation
y = a x + b faut-il
agir ?
¤ Redéfinir le segment précédent en lui donnant comme équation Y = (0.5 + cos(t)) X + 3 puis piloter t au clavier.
¤ Combiner les deux mouvements en prenant :
Y = (0.5 + cos(t)) X + 3 + cos(t).
12![]() On peut remarquer que le segment,
lorsqu’il bouge, passe par un point fixe. Quel est ce point ? Démontrer
qu’il en est effectivement ainsi.
On peut remarquer que le segment,
lorsqu’il bouge, passe par un point fixe. Quel est ce point ? Démontrer
qu’il en est effectivement ainsi.
¤ Supprimer le segment précédent.
On considère maintenant les segments d’équation Y = 0.5 X + 3 sur [ -2 ; 4 ] et Y = -2 X - 2 sur [ -6 ; -2 ]. Ils se « touchent » pour x = -2. Ils pourraient représenter un coin de voile.
Pour donner une impression de tangage, on modifie leur équation en :
Y = (0.5 + cos(t)) X + 3 et Y = (-2 + cos(t)) X - 2
Piloter t et observer.
¤ Combiner les deux mouvements en prenant :
Y = (0.5 + cos(t)) X + 3 + cos(t) et
Y = (-2 + cos(t)) X - 2 + cos(t)
13 ![]() Que dire de l’angle formé par
ces segments ?
Que dire de l’angle formé par
ces segments ?
Pour animer la figure, la méthode qui consiste à modifier tous les coefficients directeurs en ajoutant un même nombre est-elle satisfaisante ?
À chercher à la maison :
Démontrer que dans les deux derniers cas, lorsque t varie, les segments se « touchent » toujours en un point, d’abscisse -2 et d’ordonnée variable.
Dans un repère orthonormal, d’origine O on donne A (1 ; 1), A’ (1 ; 1 + e) , B (1 ; -2) et B’ (1 ; -2 + e), e étant un certain nombre réel. On passe de la droite (OA) à la droite (OA’) en ajoutant e au coefficient directeur de (OA). De même pour passer de (OB) à (OB’).
Prouver que, en général, les angles 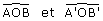 n’ont pas la même mesure.
n’ont pas la même mesure.
Aide :
Pour montrer qu’une propriété n’est pas vérifiée, il suffit de trouver un contre-exemple.
On construit le navire dans un repère orthonormal mobile par rapport au repère défini par défaut dans le logiciel et on fait bouger le repère mobile.
¤ Demander au professeur le fichier Galmob puis modifier ce fichier pour créer le mouvement.
Ce fichier contient une figure ainsi réalisée :
Dans le repère  défini par défaut (Roxy) on
a créé :
défini par défaut (Roxy) on
a créé :
- un point O, provisoirement libre,
- les coordonnées xO et yO du point O
- les points I et J de coordonnées respectives (xO + 1 ; yO) et (xO ; yO + 1).
- un point I’ provisoirement libre sur le cercle c de centre O et de rayon 1
- le point J’, image du point I’ dans la rotation de centre I’ et d’angle +90°.
Le repère
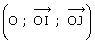
est donc le translaté du repère par défaut (Roxy) dans la translation de vecteur
 .
.
Le repère
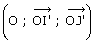
se déduit de
![]()
par rotation autour de O.
Le repère
![]()
est orthonormal et « mobile » par rapport à . ![]() .
.
En agissant sur O on translate l’image.
En agissant sur I’ on fait tourner l’image autour de O
- On a défini une variable réelle libre, t, sur l’intervalle [-15 ; 15 ] (on peut modifier l’intervalle).
Pour animer la figure en pilotant au clavier la variable t, il suffit de redéfinir les points O et I’ comme points repérés dans le repère par défaut en leur donnant des coordonnées bien choisies dépendant de t.
Par exemple, si O a pour coordonnées (t ; 0), il se déplace horizontalement quand on pilote t au clavier. S’il a pour coordonnée (2*cos(t) ; 2*sin(t)), il tourne sur le cercle de centre o et de rayon 2…
La redéfinition de I’ agit sur le tangage…