Niveau

Classe de première.

Prérequis

Notion de tangente à une courbe. Fonctions de référence.

Objectifs

Établir un lien entre le coefficient directeur de la tangente à la représentation graphique d'une fonction en un point donné, l'abscisse de ce point et l'expression algébrique définissant la fonction.

Organisation pratique

Cet imagiciel est proposé en deux versions :

L'une permet à l’élève d’effectuer un travail autonome en validant et vérifiant ses réponses : il s’agit de l’imagiciel contenu dans le pack : nbdr_auto

L’autre servira de support à un travail de recherche (collectif ou individuel) dans le cadre d’une heure de cours traditionnelle ou d’une séance de travaux dirigées ; l’imagiciel permet de visualiser un certain nombre de conjectures ; une « fiche élève » accompagne ce travail afin de noter et d’approfondir les conjectures émises à partir des situations qui sont présentées ; il s’agit de l’imagiciel contenu dans le pack : nbdr_acx

Pour fonctionner cet imagiciel nécessite l’installation des contrôles ActiveX du CREEM (logiciel gratuit) sur la machine ainsi que le réglage du niveau de sécurité d’Internet Explorer au plus bas ; il ne peut fonctionner qu’avec ce navigateur.

Description

L’imagiciel comporte trois séries d’exercices sur :

les fonctions polynômes de degré 2

les fonctions polynômes de degré 3

les fonctions définies par f(x) = a / x

les fonctions trigonométriques

ainsi qu’un exercice faisant intervenir des fonctions inconnues des élèves (les fonctions logarithme népérien et exponentielle) uniquement par leurs représentations graphiques.

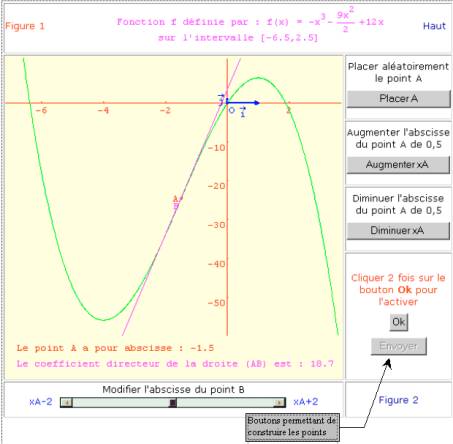
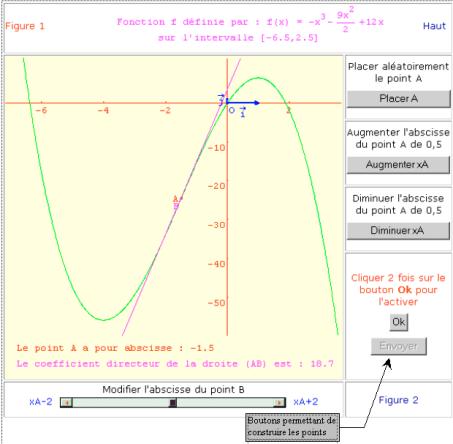
Dans chacun des exercices un premier écran présente la représentation graphique d’une fonction sur un intervalle donné ; un point A est placé au hasard sur cette représentation graphique et peut être déplacé à l’aide de boutons.

Par un autre point B de la représentation graphique on trace la droite (AB) ; le déplacement du point B sur la représentation graphique permet d’amener cette sécante (AB) en position de tangente à la représentation graphique au point A.

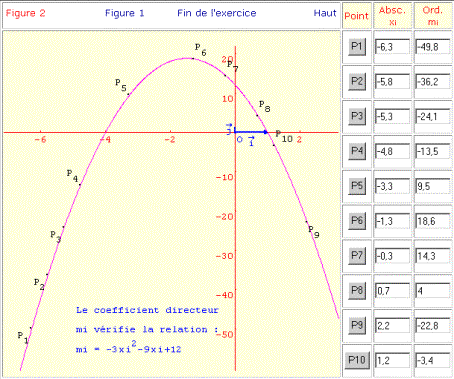
L’imagiciel affiche en permanence l’abscisse du point A ainsi que le coefficient directeur de la droite (AB) ; lorsque la droite (AB) est placée en position de tangence, la combinaison de deux boutons permet de construire dans un autre repère un point P_i dont l’abscisse sera celle du point A et l’ordonnée le coefficient directeur de la tangente au point A. Il est possible de construire ainsi 10 points P_i afin d’essayer de trouver une relation liant les coordonnées de ces points.

Les quatre étapes d’utilisation de l’imagiciel « nbdr_auto »

Installation

Décompresser le fichier nbdr_auto.zip dans le dossier de votre choix, puis à l’aide d’Internet Explorer lancer le fichier : intro.htm.

Étape 1 - Approche de la tangente au point A

Étape 2 - Visualisation de l’ensemble des points Pi

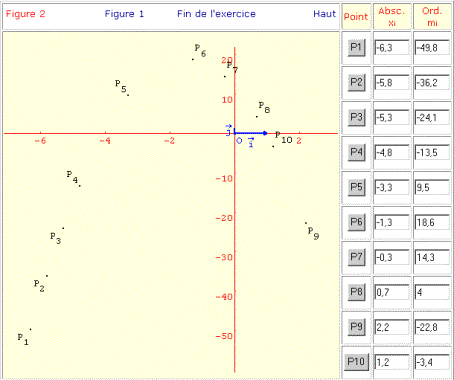
Remarque : il est possible à l’aide des boutons P_i de modifier les coordonnées d’un point.

Étape 3 - Conjecture sur la relation liant les coordonnées des points P_i

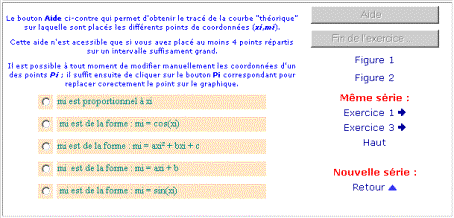
Remarques :

Le bouton Aide n’est actif que lorsqu’au moins deux points Pi ont été placés.

Il ne donne le tracé de la courbe « théorique » sur laquelle se trouvent les points Pi que lorsqu’il y a au moins 4 points placés sur un intervalle de largeur au moins 75% de celle de l’intervalle de représentation de la fonction f ; si ces conditions ne sont pas remplies on obtient l’un des deux messages suivants :

ou

Lorsque l’on a placé 10 points sur la Figure 2 à l’aide des outils automatiques il est toujours possible de modifier manuellement un des points en relevant ses coordonnées sur la Figure 1, puis en les tapant dans les cellules adéquates de la Figure 2 ; il suffit de cliquer sur le bouton du point correspondant pour que celui-ci soit corrigé.

Étape 4 - Vérification de la conjecture

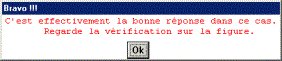
Les quatre étapes d’utilisation de l’imagiciel « nbdr_acx »

Installation

Décompresser le fichier nbdr_acx.zip dans le dossier de votre choix, puis à l’aide d’Internet Explorer lancer le fichier : intro.htm.

Étape 1 - Approche de la tangente au point A

Étape 2 - Visualisation de l’ensemble des points Pi

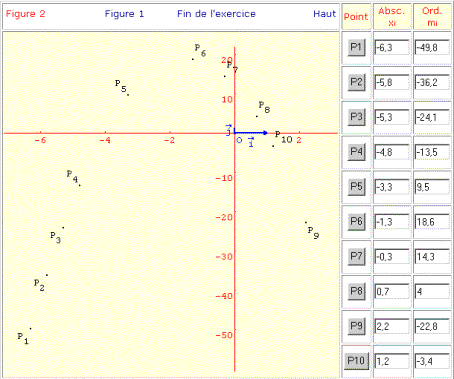
Remarque : il est possible à l’aide des boutons P_i de modifier les coordonnées d’un point.

Étape 3 - Conjecture sur la relation liant les coordonnées des points P_i

Remarques :

Le bouton Aide n’est actif que lorsqu’au moins deux points Pi ont été placés.

Il ne donne le tracé de la courbe « théorique » sur laquelle se trouvent les points Pi que lorsqu’il y a au moins 4 points placés sur un intervalle de largeur au moins 75% de celle de l’intervalle de représentation de la fonction f ; si ces conditions ne sont pas remplies on obtient l’un des deux messages suivants :

ou

Ÿ   Lorsque l’on a placé 10 points sur la Figure 2 à l’aide des outils automatiques il est toujours possible de modifier manuellement un des points en relevant ses coordonnées sur la Figure 1, puis en les tapant dans les cellules adéquates de la Figure 2 ; il suffit de cliquer sur le bouton du point correspondant pour que celui-ci soit corrigé.

Étape 4 - Utilisation de la fiche papier

Pour chacun des exercices rencontrés dans l’imagiciel il faut ensuite compléter la fiche papier jointe en indiquant à chaque fois la relation qui semble correspondre à l’observation graphique ainsi que les valeurs des différents coefficients que l’on pourra déduire des coordonnées des points Pi.

Fiche élève

Rappel

Pour chaque point A d’abscisse x_i de la représentation graphique de la fonction f on détermine le coefficient directeur m_i de la tangente en A à la représentation graphique de la fonction f. On construit ainsi un ensemble de points P_i(x_i,m_i).

Il s’agit pour chacune des fonctions étudiées de déterminer la proposition qui semble le mieux caractériser la relation reliant m_i à x_i.

Fonction polynôme de degré 2

Fonction polynôme de degré 3

Fonction définie par :

Fonction trigonométrique

Fonction inconnue