Suite récurrente sur un cercle |
|
| Équipe Académique Mathématiques |
|
Niveau
Première S et/ou Terminale S
Prérequis
Notions de base sur les suites géométriques
Objectifs
Visualiser graphiquement et numériquement un phénomène de convergence à partir d’un problème géométrique.
Organisation pratique
Ordinateur tableau noir (professeur) avec vidéoprojecteur (une utilisation en salle informatique est également envisageable) pour la première partie : durée 10 mn.
Un à deux élèves par machine pour la deuxième partie : durée 20mn.
· Fichier suicerc2.g2w utilisable à l'aide du logiciel géoplanW du creem pour la première partie.
· Fichiers tableur pour la seconde partie :
| Logiciel |
Fichier |
Remarque |
|
| Fichier élève |
Lotus 123 |
Suite cercle élève.123 |
|
| Excel 97 |
Suite cercle élève.XLS |
||
| Excel 95 |
Suite cercle élève 95.XLS |
||
| Excel 5 |
SuiCelv5.XLS |
||
| Fichier Prof |
Lotus 123 |
Suite cercle.123 |
|
| Excel 97 |
Suite cercle.XLS |
Activer les macros au lancement |
|
| Excel 95 |
Suite cercle 95.XLS |
||
| Excel 5 |
SuiCerc5.XLS |
Si les
macros ne fonctionnent pas correctement |
Description
Le travail s’effectue en trois parties :
Avec le logiciel GéoplanW on va visualiser le comportement d’une suite lorsque l’on augmente le nombre de ses termes ;
A l’aide du tableur on va ensuite conjecturer la valeur de « la limite ».
Le travail sera complété par une recherche personnelle visant à démontrer les résultats conjecturés.
Tiré du document d’accompagnement des programmes de 1re – CNDP 2001
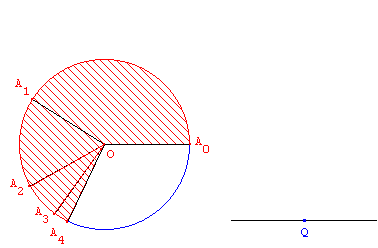
Soit q un réel de l’intervalle ]0,1] et (C) un cercle de centre O passant par un point A0. On appelle S0 l’aire du disque correspondant.
On construit le point A1 du cercle tel que l’aire S1 du secteur déterminé par l’angle A0OA1soit égale à q S0, puis le point A2 du cercle tel que l’aire S2 du secteur A1OA2 soit égale à q S1.
On réitère le processus… et on s’intéresse à la partie du disque que l’on arrive ainsi à recouvrir.
1° Partie - Avec GéoplanW (classe entière) ; durée : 10 mn.
Cette partie est uniquement une partie découverte qui sera proposée aux élèves à l’aide d’un ordinateur utilisé comme tableau noir.

Le professeur dispose de la figure correspondante qui comprend le cercle de centre O, les points A0, A1 et A2 ; les aires correspondantes sont coloriées ; un dispositif permet de faire varier la valeur du nombre q dans l’intervalle ]0,1] ou de lui affecter des valeurs remarquables : 1/2, 1/3, 1/4, …
Il dispose d’une commande préalablement construite qui, par appui sur la touche I du clavier, lui permet d’itérer le processus de construction et de faire apparaître ainsi la suite des points A3, A4, … ainsi que les surfaces correspondantes.
Il est donc aisé de visualiser le comportement de la somme des aires ainsi obtenues lors de la répétition du procédé de construction ; d’autre part la possibilité de faire varier la valeur du coefficient q soit de manière « continue », soit par choix de valeurs remarquables doit amener les élèves à conjecturer le comportement de la suite ainsi construite lorsque l’on augmente le nombre de ses termes.
Néanmoins, bien que le logiciel permette de construire une cinquantaine de points grâce au processus d’itération, il ne permet que de visualiser un comportement sans permettre de conjecturer facilement la valeur de la « limite » obtenue.
Remarque :
La liste des commandes utiles est obtenue en affichant les commentaires de la figure à l’aide de la touche F3.
2° Partie - Avec un tableur, en demi-classe : un (ou deux) élève(s) par ordinateur ; durée : 20 mn.
Le passage des élèves sur le tableur va leur permettre de construire les suites correspondant aux aires S1, S2, … ainsi qu’à la somme de ces aires et de conjecturer à la fois numériquement et graphiquement les phénomènes de convergences.
L’élève dispose d’une feuille de calcul préformatée par le professeur afin de gagner du temps dans la réalisation de l’exercice ; en particulier le professeur a préparé un graphique en secteurs dont le champ des données est :C10..C100 qui permet une visualisation immédiate au fur et à mesure de la recopie des formules.
Feuille de calcul élève (fichier : Suite Cercle Élève….)
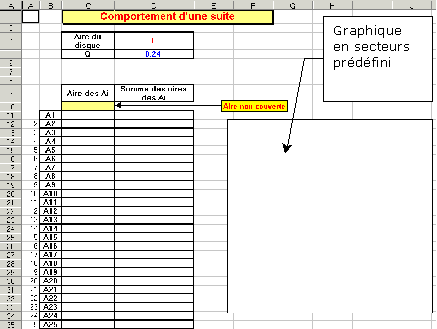
Les formules à placer au départ sont les suivantes :
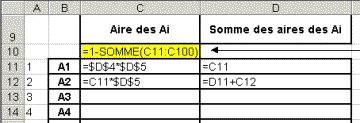
La valeur de q est placée en cellule D5 afin de pouvoir la modifier facilement et observer les changements induits par une nouvelle valeur de q.
Le professeur peut disposer d’une version améliorée de la feuille de calcul afin de faire apparaître certaines valeurs caractéristiques.
Feuille de calcul professeur (fichier suite cercle...)
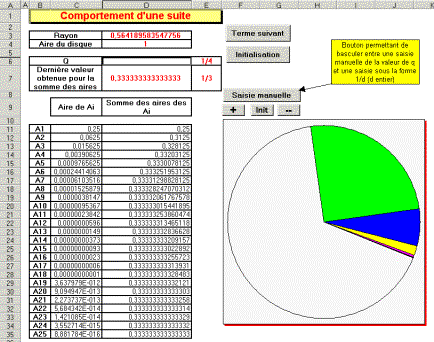
Lors du travail sur le tableur on demande à l’élève de générer les termes des deux suites récurrentes et de les recopier vers le bas afin de constater numériquement et graphiquement l’évolution du phénomène. Il doit ensuite modifier la valeur de q afin de conjecturer le lien entre cette valeur et celle de la limite qui semble être atteinte.
On peut rechercher quelle valeur donner à q afin de recouvrir ¼, la moitié ou la totalité du disque de départ.
L’élève imprime ou recopie les différents résultats observés afin de pouvoir les comparer aux résultats démontrés ultérieurement.
La version « professeur » utilisée en classe entière peut apporter une aide à la conjecture lorsque q peut s’écrire sous la forme 1/d (d entier).
3° Partie - Recherche personnelle, à la maison, puis correction et mise en forme lors de la séance suivante
Il restera ensuite à formaliser et à démontrer les résultats que l’outil informatique aura permis de conjecturer :
Ÿ Recherche de :
![]()
Ÿ Calcul de la
somme : ![]() .
.
Ÿ Recherche de :
![]()
Ÿ Lien de cette limite avec q lorsque q peut s’écrire sous la forme 1/d (d entier).