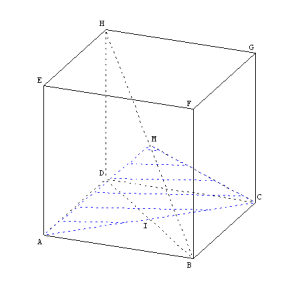
| ABCDEFGH est un cube d’arête 2 a = 4. M est un point mobile du segment [HB] ; I est le centre de la face ABCD.
On note x la distance BM.
On cherche à étudier l’aire S du triangle AMC en fonction de la position du point M. |
|
A. Observation de la variation de l’aire
Partie 1 : ouvrir le fichier « volet1.g3w »
a. On va observer l’évolution de l’aire S du triangle AMN en fonction du déplacement du point M sur [HB] ; pour déplacer le point M, appuyer sur la touche X, puis utiliser les flèches directionnelles.
b. Conjecturer le sens de variation de S.
c. Calculer les valeurs particulières de S dans chacun des cas suivants :
M est en B
M est en H
d. Vérifier ensuite à l’aide de l’imagiciel (attention : celui-ci ne donne qu’une valeur approchée de l’aire).
Partie 2 : ouvrir le fichier « volet2.g3w »
Cette figure place le plan (xoy) de face ; on va y construire des points dans le repère orthonormé d’origine O associé à ce plan (repère visualisé par ses axes).
a. Mettre les deux fenêtres en mosaïque par la commande : Fenêtre / Mosaïque.
b. Le point P a pour coordonnées (x, S). On veut obtenir la trace de ce point lorsque M se déplace sur le segment [HB] ; pour cela :
– choisir l’objet qui doit laisser sa trace : Afficher / Sélection trace …choisir le point P, puis cliquer sur OK.
– Sélectionner le mode trace en cliquant sur l’icône ![]() .
.
– Se placer sur la fenêtre « volet1.g3w » ; en déplaçant le point M à l’aide des flèches directionnelles le point P laisse sa trace dans la fenêtre « volet2.g3w ».
c. Confronter la conjecture faite précédemment à l’observation de la trace du point P. Quel est le sens de variation de S ?
d. Les coordonnées de P apparaissent dans le fenêtre « volet2.g3w » ; retrouver les résultats trouvés à la question 1.c.
B. Recherche d’un minimum
On cherche maintenant à connaître la position du point M sur le segment [HB] pour laquelle l’aire du triangle AMC est minimale.
a. Le triangle AMC étant de base [AC] de longueur constante, de quoi va dépendre l’aire de ce triangle ?
b. Lorsque M varie sur le segment [HB], à quel plan fixe appartient [IM] ?
Ouvrir le « volet3.g3w »
Cette figure place le plan (xoy) de face ; on va y construire des points dans le repère orthonormé d’origine O associé à ce plan (repère visualisé par ses axes).
Cette figure contient les valeurs a et x qui définissent le cube et la position du point M dans la figure « volet1.g3w » ; il est donc possible d’utiliser ces valeurs pour effectuer des constructions.
a. Disposer les fenêtres en mosaïque par la commande : Fenêtre / Mosaïque.
b. On veut construire dans cette figure le triangle BDH en
vraie grandeur ; pour cela il faut placer les points B, D et H par leurs
coordonnées dans le plan (xoy) afin qu’ils respectent les données de la figure
« volet1.g3w ». On utilisera la commande :
Créer / Point / Point repéré / Dans un plan (on choisira
le plan (xoy)).
c. Construire le point M sur la demi-droite [BH) se trouvant
à la distance x de B en utilisant la commande :
Créer / Point / Point repéré / Sur une demi-droite.
d. Construire le milieu I du segment [BD] en utilisant la
commande :
Créer / Point / Milieu.
e. Construire le segment [IM] en utilisant la commande :
Créer / Ligne / Segments /
Définis par 2 points.
f. En déplaçant le point M à l’aide des flèches directionnelles dans la fenêtre« volet1.g3w », observer simultanément les fenêtres « volet2.g3w » et « volet3.g3w » et conjecturer la position de M pour laquelle S est minimale.
g. Démontrer cette conjecture.
h. Calculer la valeur de x pour laquelle l’aire S est minimale ainsi que la valeur de cette aire.