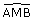 = 60° (les élèves pourraient penser à un triangle équilatéral)
= 60° (les élèves pourraient penser à un triangle équilatéral)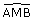 = 60° et AMB non équilatéral
= 60° et AMB non équilatéral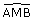 = 45° (les élèves pourraient penser à un triangle rectangle isocèle en A ou en B)
= 45° (les élèves pourraient penser à un triangle rectangle isocèle en A ou en B)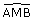 = 45° et AMB non rectangle.
= 45° et AMB non rectangle.| Constructions à la règle et au compas |
| Équipe Académique Mathématiques, Bordeaux, janvier 2002 |
Destination
Professeurs
Type
Papier
Niveau
Première L, option facultative
Extraits du programme
Première L enseignement optionnel
Contenus
Modalités
Commentaires
Géométrie plane
Constructions et tracés ("à la règle et au compas")
Constructions de polygones réguliers (à n côtés pour n = 3, 4, 6, 8, 12).
Problèmes de constructionOn s'appuiera sur les transformations étudiées jusqu'en seconde, y compris les agrandissements et réductions ; on rappellera avec précision les propriétés utilisées.
On utilisera les propriétés des angles géométriques (y compris le théorème de l'angle inscrit).
On traitera des exemples tels que : cercle de rayon donné passant par un point donné et tangent à une droite donnée (ou tangents à deux droites) ; cercle tangent à trois droites données ; triangle équilatéral inscrit (resp. circonscrit) dans un triangle donné ; construction de figures semblables à une figure donnée ; carré "inscrit" dans un demi-disque, dans un triangle ; tangente commune à deux cercles.
Dans tout ce paragraphe, on articulera avec soin tracés effectifs et justifications.
On utilisera en particulier les logiciels de géométrie : ceux-ci dispensent des problèmes de tracés et leur utilisation nécessite l'explicitation a priori des propriétés traduisant l'énoncé. Cette utilisation s'intègre donc tout à fait dans la démarche de démonstration souhaitée ici.
On pourra expliciter la méthode qui consiste à abandonner dans un premier temps une des contraintes du problème.
Commentaires
Le premier document « Constructions à la règle et au compas » donne les définitions universitaires de « point, droite et cercle constructibles à la règle et au compas ». Elle est extraite du livre de J.C. Carrega « Théorie des corps ; la règle et le compas » éditions Hermann 1981. Il n’est bien évidemment pas question de la donner aux élèves. Cependant, le deuxième document intitulé « Une idée de démarrage … » donne une progression possible du cours qui reprend, dans la définition de Carrega, l’idée de « points de base ».
Avec successivement deux, puis trois et enfin quatre points de base, on liste les constructions élémentaires c’est-à-dire celles que les élèves n’auront pas à détailler dans leurs explications ; après chaque cas, des exercices sont proposés.
Auteur
Équipe Académique Mathématiques, Bordeaux, janvier 2002
Constructions à la règle et au compas : définition
Définition donnée par J.C Carrega dans : « Théorie des corps ; la règle et le compas » éditions Hermann 1981.
Soit P un plan euclidien et (B) un sous ensemble fini de P
ayant au moins deux éléments.
Les éléments de B sont appelés points de base.
Un point M de P est dit constructible à la règle et au compas à partir de (B) s’il existe une suite finie de points de P se terminant par M : M1, M2,….., Mn = M telle que pour tout i, 1 £ i £ n, Mi est un point d’intersection :
ces droites et cercles étant obtenus à l’aide de l’ensemble Ei = (B) U {M1, M2,….,Mi-1} de la façon suivante :
Une droite passant par deux points constructibles est dite constructible.
Un cercle centré en un point constructible et ayant pour rayon la distance entre deux points constructibles est dit constructible.
Remarque
Chaque point de base est constructible à la règle et au compas à partir de (B). Cela pourrait être une simple convention venant compléter la définition précédente ; en fait cette convention n’est pas nécessaire car si B î (B) et si B’ est un autre point de (B) alors B est un point d’intersection de la droite (BB’) et du cercle de centre B’ et de rayon BB’.
Une idée
de démarrage du cours
sur les constructions et tracés à la règle et au compas
Construction à larègle et au compas :
définition par questions réponses
Construction à la règle et au compas : le pourquoi
Constructions élémentaires à partir de deux points de base A et B
Exercices possibles à ce stade du cours
1) Deux points A et B sont donnés sur la feuille.
Construire à la règle et au compas un point M tel que
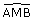 = 60° (les élèves pourraient penser à un triangle équilatéral)
= 60° (les élèves pourraient penser à un triangle équilatéral)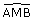 = 60° et AMB non équilatéral
= 60° et AMB non équilatéral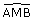 = 45° (les élèves pourraient penser à un triangle rectangle isocèle en A ou en B)
= 45° (les élèves pourraient penser à un triangle rectangle isocèle en A ou en B)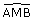 = 45° et AMB non rectangle.
= 45° et AMB non rectangle.2) Un cercle C de centre O et un point A de ce cercle sont dessinés
sur la feuille.
Construire à la règle et au compas la tangente en A au cercle C.
3) Un cercle C de centre O et un point A extérieur à C sont dessinés
sur la feuille.
Construire à la règle et au compas une tangente au cercle C, passant par A.
Constructions élémentaires à partir de trois points de base A, B et C
(Sauf dans la dernière construction, les points A, B et C peuvent être alignés)
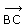 .
.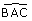
Exercices possibles à ce stade du cours
1) Trois points non alignés A, B et C sont donnés sur la feuille. Construire
2) Un « rond », c’est-à-dire un
cercle dont on a perdu le centre est dessiné sur la feuille.
Construire à la règle et au compas le centre de ce cercle.
3) Tracer l’image d’une droite ou d’un cercle par translation ou symétrie axiale.
Constructions élémentaires à partir de quatre points de base A, B, C et D
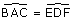 (report d’angle).
(report d’angle).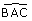 .
.Exercice possible à ce stade du cours
Quatre points A, B, C et D sont donnés sur la feuille.
Construire à la règle et au compas un quadrilatère dont A, B, C et D sont les
milieux des côtés.
Partage d’un segment [AB]
Construire des points sur le segment [AB] le partageant en n segments de même longueur en prenant successivement n = 5 (Thalès), n = 3 (Thalès ou propriété du centre de gravité), n = 4 (Thalès ou trois milieux).
Exercices possibles à ce stade du cours.
Deux points A et B sont donnés sur la feuille.
Construire à la règle et au compas un point M tel que
Construction à la règle et au compas de polygones réguliers
1) Construire un triangle équilatéral
2) Construire un carré et un hexagone, un octogone un dodécagone réguliers (voir le document d’accompagnement).
On peut faire remarquer aux élèves que certains polygones
réguliers ne sont pas examinés mais pour des raisons différentes :
pentagone : possible mais trop difficile ( ? )
heptagone, nonagone , … : impossible.
Théorème de Gauss : un polygone régulier à n cotés est constructible à la règle et au compas, si et seulement si, la décomposition en facteurs premiers de n est de la forme 2ap1p2…pk où p1, p2, …, pk sont des nombres premiers de Fermat distincts et a un entier naturel quelconque.
Rappel : les nombres premiers de Fermat s’écrivent
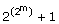 mais les nombres de cette
forme ne sont pas tous premiers.
mais les nombres de cette
forme ne sont pas tous premiers.
Ainsi, les nombres de Fermat 3, 5, 17, 257, 65 537 successivement obtenus pour m = 0, 1, 2, 3, 4 sont premiers mais pour m = 5 par exemple, le nombre 4 294 967 297 ne l’est plus (4 294 967 297 = 641 ´ 6 700 417).
Conséquence : la construction d’un polygone régulier à n côtés (n compris entre 3 et 50) n’est possible que pour n égal à 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48.
Exercices possibles à ce stade du cours
Tous les exercices du document d’accompagnement