Fonctions de COOB-DOUGLAS en microéconomie
	Équipe académique maths Bordeaux, juin 2002

 

Définitions

Une entreprise achète deux produits (input) en quantité x et y avec lesquels elle fabrique un troisième produit qu’elle vendra (output), en quantité z.

Bien sûr, z est fonction de x et de y (fonction de production).

Cette fonction de production est de type Coob-Doublas lorsque : 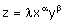 avec a, b et l constantes réelles, l > 0, a > 0, b > 0.

 

Forme des surfaces de type Coob-Douglas

Les courbes isoquantes (z constante non nulle) ont une équation de la forme
.

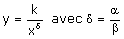Si a = b, ces courbes sont des hyperboles d’équation

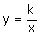
 et l’ensemble de ces hyperboles isoquantes est indépendant de a.

Intersection avec le plan xOz d’équation y = 0 : c’est le demi-axe Ox.

Intersection avec le plan xOy d’équation z = 0 : c’est Ox È O y.

Intersection avec le plan yOz d’équation x = 0 : c’est le demi-axe Oy.

Il est donc impossible d’imaginer cette surface en regardant son intersection avec les plans de coordonnées ; d’où l’idée de chercher son intersection avec le plan P d’équation y = x .

.

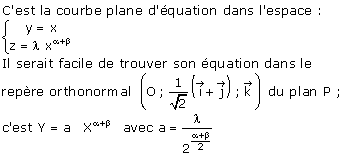Pour la forme de cette dernière courbe, on distingue trois cas :

si a + b = 1, alors cette courbe est une droite de coefficient directeur a avec  ;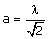

si a + b < 1, alors cette courbe est de type « racine » ;

si a + b > 1, alors cette courbe est de type « puissance > 1 ».

L’ensemble des points dont les coordonnées vérifient 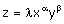 est convexe dans les deux premiers cas mais ne l’est plus dans le troisième.

Dans le cas particulier où a et b sont égaux, que ce soit par exemple à 0,5 ou 1 ou 0,2, la visualisation de l’ensemble des hyperboles isoquantes ne renseigne pas sur la convexité de la surface puisqu’il est indépendant de a.

Interprétation économique de ces trois cas

Si les quantités x et y achetées par l’entreprise sont multipliées par un même réel k,  alors la quantité vendue z sera quant à elle multipliée par k ^{a + b} . C’est ce que les économistes appellent les rendements d’échelle.

si a + b = 1, les rendements d’échelle sont constants ;

si a + b < 1, les rendements d’échelle sont décroissants ;

si a + b > 1, les rendements d’échelle sont croissants.